霍夫曼（Huffman）压缩编码算法

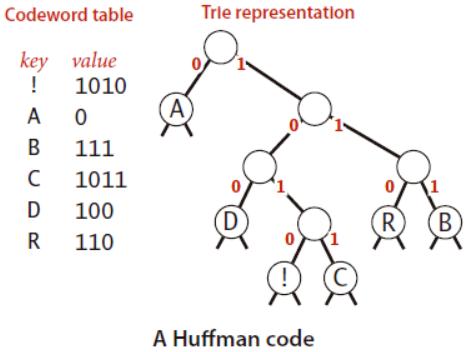
霍夫曼编码（Huffman Coding），又译为哈夫曼编码、赫夫曼编码，是一种用于无损数据压缩的熵编码（权编码）算法，由大卫·霍夫曼在1952年发明。

霍夫曼编码算法的思想：通过不定长编码的方式，使出现频率越高的字符对应短码，出现频率低的字符对应长码，以此来达到无损压缩的效果（用较少的比特表示出现频率高的字符，用较多的比特表示出现频率低的字符）。而且，任一字符编码都不是其它字符编码的前缀，编码后的bit stream不需要分隔符。

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和。

相同的排序队列，构造的Huffman Tree不唯一，但不影响编码压缩效率。比如当将那个节点合并成一个根节点的时候，哪个在左，哪个在右，虽然影响某个字符的编码，但是不影响编码长度，也不影响编码压缩效率。

通过遍历Huffman Tree，就可以得到每一个叶子结点的code。对于根节点，规定左边的路径是0，右边的路径是1，这样得到的code，就是一组01序列。（当然也可以规定左边路径为1，右边路径为0，这也是为什么Huffman编码不唯一，但长度唯一）

由于构建Huffman Tree是从底向上进行的，出现频率越大的叶子结点，越靠近root。因此，出现频率越高的叶子结点，其code越短。

每一个叶子结点，其code唯一，而且不与任何其它code的前缀重复！

研究发现，可以通过规范化Huffman树，在保持压缩效率一致的前提下，减少存放Huffman树本身的空间。

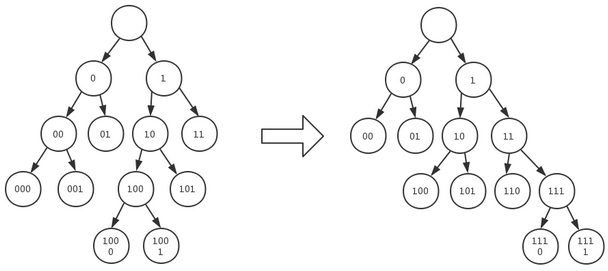
Huffman树经过规范化处理后，只需要保存高度h，以及对应的叶子节点数：

规范后的Huffman树，还有个特性，可以快速获取叶子结点的codeword：

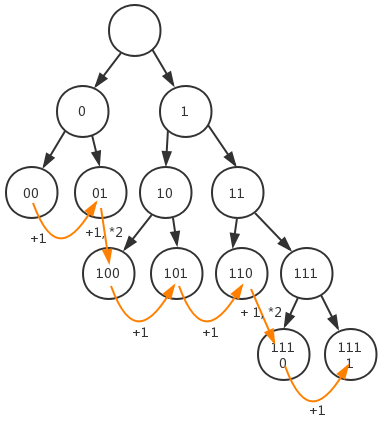
从左到右，从上到下遍历叶子结点，按这个顺序，它们的codeword就是 +1，和+1后*2的关系。最后特别注意：codeword的长度与huffman树叶子所在高度相同。jpeg压缩就用到了这些技术。