-- TOC --
图论中最基础的搜索算法,宽度优先搜索,BFS。它的实现没有递归,因此更容易被理解。BFS同时适用于有向图和无向图。
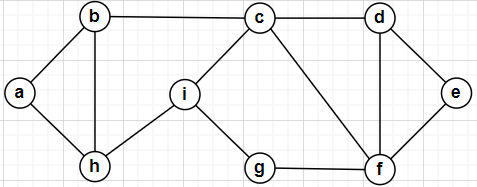
下面是一个无向图的示例:

BFS算法同时也是Unweighted Graph的Single Source Shortest Path(SP)算法!由于Edge都没有Weight(也可认为这是所有Weight都相等的特例),Shortest Path就是数Edge的数量。一般在具体实现时,算法会记录每个节点的父节点和经过的Edge数量,BFS算法最后会形成一颗BFS Tree,Root节点就是起始节点,Root到每一个Tree中的节点,都具有SP性质。BFS Tree也是一颗Unweight Graph的MST,由于可以认为所有Edge的Weight都相等,在选Edge时就可以随意,最后生成的Tree一定是MST。
对于Unweighted Graph而言,只要联通,它即是SP,也是MST。
下面是个稍有些冗余的参考实现。经典BFS的实现,核心数据结构就是一个Queue:
G = {
'a': ('b','h'),
'b': ('a','h','c'),
'c': ('b','i','f','d'),
'd': ('c','f','e'),
'e': ('d','f'),
'f': ('g','c','d','e'),
'g': ('i','f'),
'h': ('a','b','i'),
'i': ('h','c','g'),
}
from collections import deque
class Vertex:
def __init__(self, name, dist, parent):
self.name = name
self.dist = dist
self.parent = parent
def __repr__(self):
p = self.parent.name if self.parent is not None else str(None)
return f'{self.name}-{self.dist}-{p}'
def BFS(G, s):
""" Breadth-First Search """
assert s in G
q = deque()
root = Vertex(s, 0, None)
visited = [root]
q.append(root)
while q:
v = q.popleft()
# visit v here
for nbv in G[v.name]:
# check if nbv is visited
for _v in visited:
if _v.name == nbv:
break
else: # nbv is not visited
nv = Vertex(nbv, v.dist+1, v)
visited.append(nv)
q.append(nv)
return root, visited
print("tranvers BFS start from a")
print(BFS(G,'a'))
print("tranvers BFS start from i")
print(BFS(G,'i'))
print("tranvers BFS start from f")
print(BFS(G,'f'))
输出:
tranvers BFS start from a
(a-0-None, [a-0-None, b-1-a, h-1-a, c-2-b, i-2-h, f-3-c, d-3-c, g-3-i, e-4-f])
tranvers BFS start from i
(i-0-None, [i-0-None, h-1-i, c-1-i, g-1-i, a-2-h, b-2-h, f-2-c, d-2-c, e-3-f])
tranvers BFS start from f
(f-0-None, [f-0-None, g-1-f, c-1-f, d-1-f, e-1-f, i-2-g, b-2-c, h-3-i, a-3-b])
复杂度:\(\Theta(V+E)\)
每个Vertex访问一次,每个Edge访问两次!
本文链接:https://cs.pynote.net/ag/graph/202404211/
-- EOF --
-- MORE --