11. Container With Most Water，最大水容器

这段话有点费解：一个名叫height的integer array，这个array中的数字表示height，array的长度为n，这个array模拟了n条垂直线，第i条线的坐标是(i,0)和(i,height[i])。

找到两条垂线，结合x轴，形成一个矩形区域，目标是使得这个矩形区域的面积最大，返回最大值。（假设这个矩形框用来装水，上面那条横线也需要是水平的）

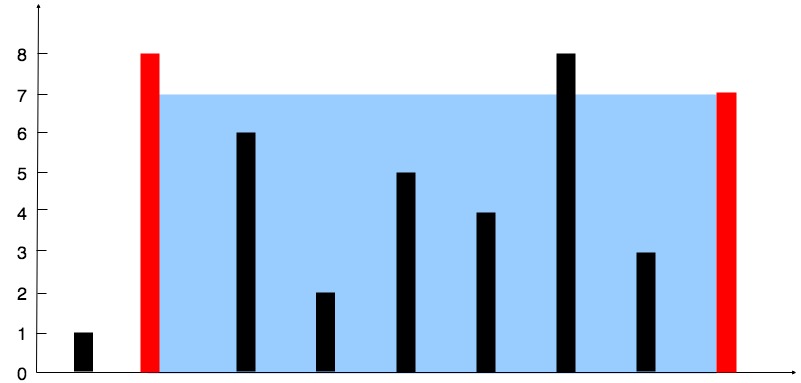
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water the container can contain is 49 (7x7).

Input: height = [1,1]
Output: 1 (1x1)

思路00

通过遍历x轴，两重循环，可以遍历出所有的container大小，最后一定可以得到一个最大值，但这是个\(O(N^2)\)的解法。

思路01

控制面积有两个维度，width和height，从大到小遍历width时，也在逐渐推高需要的height值，如果需要的height值大于了最大height，此时就可以结束了。

import math


class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_height = max(height)
        num_vlines = len(height)
        width = num_vlines - 1
        max_area = 0
        while True:
            for i in range(num_vlines-width):
                h = min(height[i],height[i+width])
                area = width * h
                if area > max_area:
                    max_area = area
            width -= 1
            if width == 0:
                break
            need_height = math.ceil(max_area/width)
            if need_height > max_height:
                break

        return max_area

这个思路比前面的在一般情况下会快一点，但依然是\(O(N^2)\)级别，依然TLE.....:(

Two Points

在一个具有某种顺序的序列中寻找两个点，这两个点的某些属性能够满足某一特定的条件，一般是先取左右两个点，然后逐渐向中间靠拢。复杂度：\(O(N)\)

比如：在一个有序数组里，寻找两个数，让他俩的和等于某个具体的值。LeetCode第1题，我有尝试这个思路的实现。

这一题也可以采用这个思路：虽然height数组没有排序，但是当width缩小后，height必须需要增大，才能够计算出更大的面积。因此，这两个点的变动，就可以按照往height增大的方向进行。

Python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area = 0
        lo = 0
        hi = len(height) - 1
        while lo < hi:
            area = min(height[lo],height[hi]) * (hi-lo)
            if area > max_area:
                max_area = area
            if height[lo] < height[hi]:
                lo += 1
            else:
                hi -= 1
        return max_area

#define MIN(a,b)   (a<b?a:b)

int maxArea(int* height, int heightSize){
    int max = 0;
    int lo = 0;
    int hi = heightSize - 1;
    while(lo < hi){
        int area = MIN(height[lo],height[hi]) * (hi-lo);
        if(area > max)
            max = area;
        if(height[lo] > height[hi])
            --hi;
        else
            ++lo;
    }
    return max;
}

C++

class Solution {
public:
    int maxArea(vector<int>& height) noexcept{
        int n {static_cast<int>(height.size())};
        int max {};
        int lo {};
        int hi {n-1};
        while(lo < hi){
            int area {min(height[lo],height[hi])*(hi-lo)};
            if(area > max)
                max = area;
            if(height[lo] > height[hi])
                --hi;
            else
                ++lo;
        }
        return max;
    }
};

贪心算法（Greedy）

也许用Two Pointer来描述本题的思路，不够准确。本题的得分点是贪心算法，Greedy Algorithm。

所谓Greedy，即在每一步计算过程中，都选择当前最优的解，即贪心！本题首先计算width最大情况下的area，每一步都意味着width在缩小，因此height必须沿着增大的方向更新。本题只是模拟了Two Pointer的代码结构，实际上是贪心算法的内核。

通过每一步计算最优解，来得到最后的结果，这就是贪心算法的思想。如果构建每一步的计算，还需要其它技巧。需要了解，并非所有的问题，都适合使用贪心的策略。