Last Updated: 2024-05-03 14:56:00 Friday
-- TOC --
KNN算法,K最近邻(K-Nearest Neighbors),是一种分类算法,1968年由Cover和Hart提出。该算法的思路是:如果一个测试样本与数据集中的K个样本最相似,这K个样本中的大多数属于某一个类别,则该测试样本也就属于这个类别了。
KNN算法的特点是:
图像分类的任务,没有用KNN算法的,原因见下文分析。
KNN算法不仅可以用于分类,还可以用来做回归(regression),思路是:测试样本的某个属性值,可以直接用其K个最邻近的数据集中样例的相同类别属性值求平均。
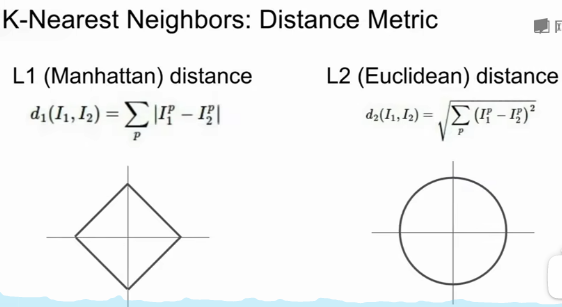
Nearest是什么?一般采用欧氏距离或者曼哈顿距离,即L2范数或L1范数。这就要求所有的数据都要用vector来表示,这样就可以计算距离,多维空间中两个点之间的距离。Euclidean距离更加unforgiving,某个维度的过大的差对最后结果的影响更大。manhattan距离的计算量会小一点,但其并非直线距离,有些反直觉,如下图:

L1距离计算每个维度差的绝对值的和,上图的正方形,表示此正方形上任意一个点到原点的L1距离都相等。L2距离计算每个维度差的平方和开根号,上图的圆形,表示此圆形上任意一点到原点的L2距离都相等。
如果坐标系发生变化,比如旋转,会影响L1距离,但不会影响L2距离(坐标系的平移不会影响L1距离)。这是选择那种距离的一个考虑因素。
假设我们有两个点,A(2,2)和B(4,4),在原始的笛卡尔坐标系中,他们的L1距离是 |2-4| + |2-4| = 4。然而,如果我们将坐标系旋转45度,那么A和B的坐标会变成A'(2.83,0)和B'(0,2.83),他们的L1距离将变成 |2.83-0| + |0-2.83| = 5.66。所以,改变坐标系可以改变两点之间的L1距离。但这并不意味着L1距离在所有情况下都不是一个好的距离度量。事实上,它在许多应用中表现得非常好,特别是当我们希望捕捉各个维度上的差异,而不仅仅是两点的直线距离时。
KNN算法模型中有两个hyperparameter需要决策:
hyperparameter的定义:choices about the algorithm that we set rather than learn。选择hyperparameter要看任务场景(problem-dependent),测试,然后选出一个你认为最好的。确定hyperparameter的时候,要使用unseen data作验证测试,所以我们一般会将数据分成三分,train,validation(unseen data)和test(final report)。
K的最小取值是1,此时数据集中谁最近,测试样本就跟它的类别一样。K的最大理论值是全体数据集的数量N,此时,全体数据集N中,哪个类别的样本数量最多,测试样本就属于哪一类,这显然是有问题的,模型过于简单。
KNN中的K值选取对K近邻算法的结果会产生重大影响。如李航博士的书「统计学习方法」上所说:如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,学习近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是学习的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合。如果选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。K=N,则完全不可取,因为此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的类,模型过于简单,忽略了训练实例中大量有用信息。在实际应用中,K值一般取一个比较小的数值,例如采用交叉验证法来选择最优的K值。
K值越小越容易overfitting,K值越大预测效果就越差,因为与测试样本较远的数据也在发挥作用。想象一个分布不均衡的数据集,有一个类别A只有较少的数据,另一个类别B有很大量的数据,此时如果K值很大,预测的结果就会严重偏向B,仅仅只是因为B的样本比较多而已。
KNN算法属于监督学习,但其实并没有真正的学习过程,有人说它是惰性学习(lazy learning)。在数据集和测试样本都准备好的时候,KNN直接计算测试样本与数据集中样本的距离,选择最好的K个,然后得出预测结果。预测的过程,就是学习的过程,因此,KNN在做预测的时候,计算量会很大。仔细想这个过程,KNN算法还有一个特点,即结果可重复,对于每一个测试样本,只要数据集不变,每一次测试的结果一定是一样的!
KNN算法不会用在图像分类任务上,原因如下:
Curse of Dimesionality,维度的诅咒。要让KNN算法很好的工作,需要让高维空间中的样本分布均匀且密集,否则可能出现预测样本与其邻近样本间的距离非常远,这会让KNN算法的效果变差。但图像数据维度非常高(每个像素点的每个颜色值,都算一个维度),难以实现均匀且密集的分布。(KNN算法更适合低维度的数据集)
我想起了曾经写的一个小功能,就是用L1距离来判断视频流中的前后帧的相似度。虽然也存在上述问题,但在实时视频流这个场景,这个问题的严重性要低不少,因为每一帧画面的变化都是自然发生的。
我自己曾经做过一些测试,下面直接记录当时的一些结果,代码就不公开了。
在K=10的时候,将KNN用于MNIST和FMNIST两个数据集,测试的结果如下图:
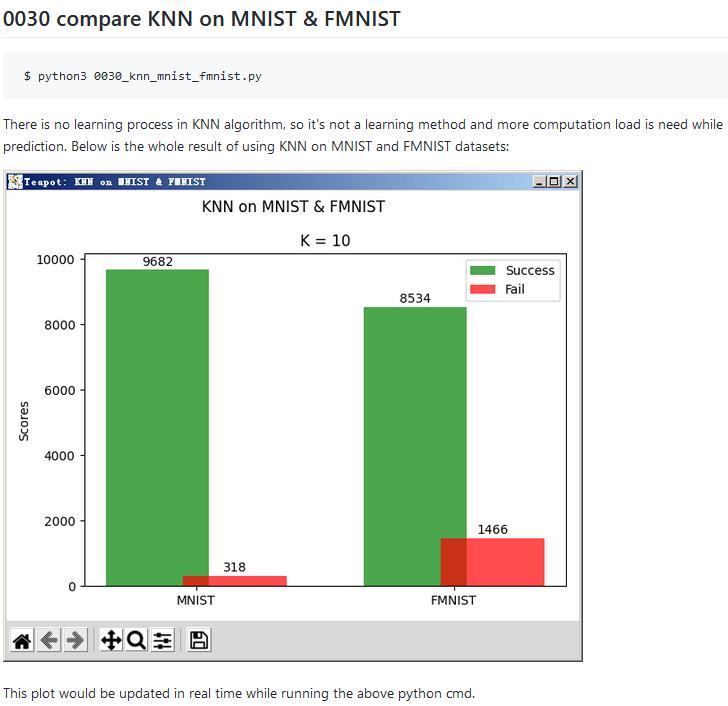
后来,我又写了一段代码,主要是想知道,对于这两个有10个分类的数据集,K的最佳取值是多少。这段代码计算K从1到500时,每一个K的取值,在两个数据集上得到的预测正确率。代码经过一定程度的优化,但还是需要运行一小会儿,主要开销是在计算每一个待预测点与训练集内60000个点的L2范数(欧式距离)。下面是运行结果:
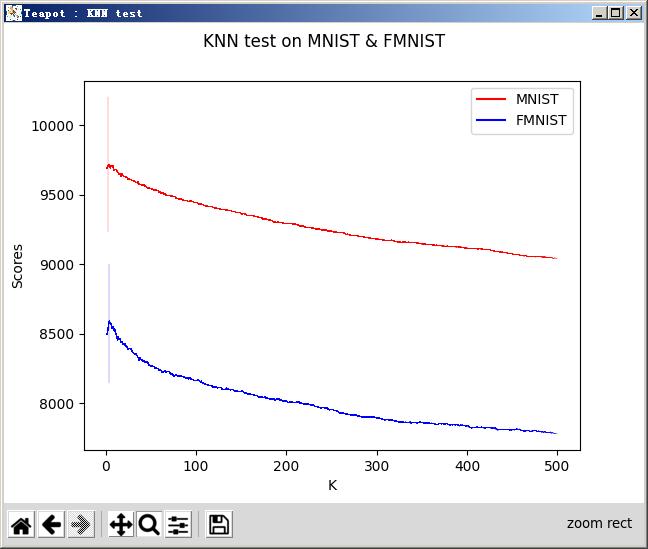
结果领人惊讶,K的最佳取值出奇地小。
3和4都没有到10个分类的一半!
而且,我们还能观察到,K值越大,预测效果越差。上图的两条曲线,呈现出单边下降的态势。
后来看到cs231n课程使用CIFAR-10数据集,跑KNN算法用于教学,准确率只能到40%左右。这就是不同数据集带来的差异了。CIFAR-10是RGB数据,而MNIST和FMNIST只有灰度,CIFAR-10数据的维度比MNIST要高很多。这就是前者在应用KNN算法时,效果很差的原因(维度的诅咒)。CIFAR-10数据的维度更高,使用L2距离来判断,相似的误差很大(背景的相似颜色有决定性作用)。
下面是个人整理的KNN计算代码,用在了计算CIFAR-10数据集上:
import os
import pickle
import time
import numpy as np
# download cifar-10 dataset if not avaiable
cmd = """\
if [ ! -d "cifar-10-batches-py" ]; then
wget http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz -O cifar-10-python.tar.gz
tar -xzvf cifar-10-python.tar.gz
rm cifar-10-python.tar.gz
fi"""
import subprocess
proc = subprocess.run(cmd, shell=True, capture_output=True)
if proc.returncode != 0:
print('==== STDOUT ====')
print(proc.stdout)
print('==== STDERR ====')
print(proc.stderr)
else:
print('cifar-10 dataset is ready!')
def load_CIFAR_batch(filename):
""" load single batch of cifar """
with open(filename, "rb") as f:
datadict = pickle.load(f, encoding='latin1')
X = datadict["data"]
Y = datadict["labels"]
# use np.uint8 to save memory
X = X.reshape(10000,-1).astype(np.uint8)
Y = np.array(Y, dtype=np.uint8)
return X, Y
def load_CIFAR10(ROOT):
""" load all of cifar-10 """
xs = []
ys = []
for b in range(1, 6):
f = os.path.join(ROOT, "data_batch_%d" % (b,))
X, Y = load_CIFAR_batch(f)
xs.append(X)
ys.append(Y)
Xtr = np.concatenate(xs)
Ytr = np.concatenate(ys)
Xte, Yte = load_CIFAR_batch(os.path.join(ROOT, "test_batch"))
return Xtr, Ytr, Xte, Yte
Xtr, Ytr, Xte, Yte = load_CIFAR10('cifar-10-batches-py')
print(f'{Xtr.shape=}')
print(f'{Ytr.shape=}')
print(f'{Xte.shape=}')
print(f'{Yte.shape=}')
print(f'{Xtr.dtype=}')
print(f'{Ytr.dtype=}')
print(f'sizeof Xtr is {Xtr.size*Xtr.itemsize/1024/1024}M')
print(f'sizeof Ytr is {Ytr.size*Ytr.itemsize/1024/1024}M')
class KNN():
""" a KNN classifier with L2 distance """
# On CPU:
# np.float32 is faster than np.float64, and it only use half the memory.
def train(self, X, Y, dtype=np.float32):
"""
Train the classifier. For k-nearest neighbors this is just
memorizing the training data.
Inputs:
- X: A numpy array of shape (num_train, D) containing the training data
consisting of num_train samples each of dimension D.
- y: A numpy array of shape (N,) containing the training labels, where
y[i] is the label for X[i].
- dtype:
"""
self.X_train = X
self.Y_train = Y
self.dtype = dtype
self.dists = None
def calc_l2_dists(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
self.sdists: A numpy array of shape (num_test, num_train) where sdists[i, j]
is the arg-sorted Euclidean distance fro the ith test vector.
"""
# in-place modification and explicit del are both for memory save
del self.dists
num_test = X.shape[0]
num_train = self.X_train.shape[0]
Xdt = X.astype(self.dtype)
Xtr_T_dt = self.X_train.T.astype(self.dtype)
# don't use just a, I don't know why...!?
a2 = np.reshape(np.sum(Xdt**2,axis=1),(num_test,1)) @ \
np.ones((1,num_train),dtype=self.dtype)
a2 += np.ones((num_test,1),dtype=self.dtype) @ \
np.reshape(np.sum(Xtr_T_dt**2,axis=0),(1,num_train))
a2 -= (Xdt @ Xtr_T_dt) * 2
del Xdt
del Xtr_T_dt
a2 = np.sqrt(a2)
self.sdists = np.argsort(a2).astype(np.uint16)
def _calc_dists_slow_right(X_train, X, dtype):
num_test = X.shape[0]
num_train = X_train.shape[0]
dists = np.zeros((num_test, num_train), dtype=dtype)
for i in range(num_test):
for j in range(num_train):
t = X_train[j,:].astype(dtype) - \
X[i,:].astype(dtype)
dists[i,j] = np.linalg.norm(t)
return dists
def _calc_l2_dists_slow_right(self, X):
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train), dtype=self.dtype)
for i in range(num_test):
for j in range(num_train):
t = self.X_train[j,:].astype(self.dtype) - \
X[i,:].astype(self.dtype)
dists[i,j] = np.linalg.norm(t)
return np.argsort(dists).astype(np.uint16)
def predict(self, X, k):
"""
Calculate a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = X.shape[0]
closest_y = self.Y_train[self.sdists[:,:k]]
return np.array([np.argmax(np.bincount(closest_y[i]))
for i in range(num_test)],dtype=self.Y_train.dtype)
def _predict_slow_right(self, X, k):
num_test = X.shape[0]
y_pred = np.zeros(num_test, dtype=self.Y_train.dtype)
for i in range(num_test):
closest_y = [self.Y_train[j] for j in self.sdists[i,:][:k]]
label_dict = {u:v for u in range(10) if (v:=closest_y.count(u))!=0}
y_pred[i] = sorted(label_dict,key=lambda x:label_dict[x],reverse=True)[0]
return y_pred
测试代码:
# test code
print('create knn object...')
knn = KNN()
print('train...')
knn.train(Xtr[:5000,:], Ytr[:5000])
print('calculate L2 distance for all...')
tic = time.time()
knn.calc_l2_dists(Xte[:1000,:])
print(time.time() - tic)
tic = time.time()
sdists = knn._calc_l2_dists_slow_right(Xte[:1000,:])
print(time.time() - tic)
print('due to diff calc path, diff:', np.sum(knn.sdists!=sdists))
print('predict...')
for i in range(1,100):
y_pred = knn.predict(Xte[:1000,:],i)
y_pred_s = knn._predict_slow_right(Xte[:1000,:],i)
assert (y_pred==y_pred_s).all()
print('ok')
以上这段代码,在性能问题上挣扎了好久:
K取从1到500,看一下结果:
print('create knn object...')
knn = KNN()
print('train...')
knn.train(Xtr, Ytr)
print('calculate L2 distance for all...')
tic = time.time()
knn.calc_l2_dists(Xte) # >50s in my 8G old machine
print(time.time() - tic)
x = [i for i in range(1,500)]
acc = []
for i in x:
y_pred = knn.predict(Xte,i)
acc.append(np.sum(y_pred==Yte))
在我的8G内存的机器上,大概50多秒就能算完,最后得到图形:
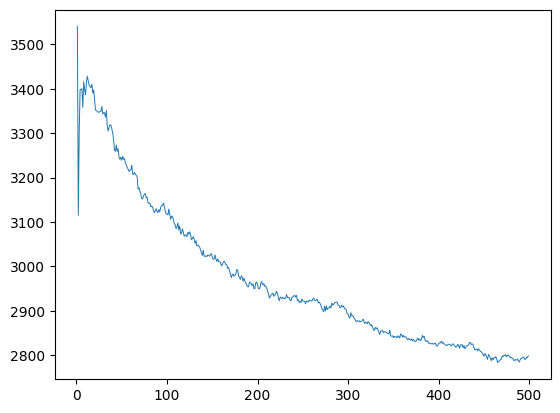
这是完整CIFAR-10数据上的结果。一样,K越大越不准确。而且由于数据更复杂,最大准确度很非常低。K=1的时候取到最大值,然后剧烈震荡了几个K值,就一路向下。
本文链接:https://cs.pynote.net/ag/ml/202210011/
-- EOF --
-- MORE --