Last Updated: 2023-08-16 04:13:49 Wednesday
-- TOC --
支持向量机(SVM,Support Vector Machines)是一种二分类模型,属于监督学习类的著名的机器学习算法,当样本的特征向量被提取并映射为空间中的点后,SVM算法的目的,就是想要画出(训练)一个超平面(hyperplane),以最好地将样本分为两类,当有了新的样本时(预测),这个hyperplane就能做出很较好的二分类判断。
hyperplane是高维空间中的平面,在二维空间是一条线,在三维空间是一个面(plane),高维空间将其称为hyperplane。hyperplane是线性的。
所谓特征向量(feature vector),可以理解为样本的一系列属性值(也称为特征值),组合在一起形成一个向量,以方便计算。对于图像而言,将RGB三个通道的数据作flatten后得到的向量,就是最简单粗暴的特征向量。
SVM最早是由 Vladimir N. Vapnik和 Alexey Ya. Chervonenkis在1963年提出,目前的版本(soft margin)是由 Corinna Cortes和 Vapnik在1993年提出(Hinton抛出BP算法是1986年),并在1995年发表。深度学习(2012)出现之前,SVM被认为机器学习中近十几年来最成功,表现最好的算法。也是由于SVM算法比浅层神经网络算法更好用,导致了一次AI寒冬。
SVM算法可以应用于分类,回归,异常值检测(outliers detections)。
在高维空间,能够将样本点划分为两类的hyperplane可以有无数多个。那么,如何定义最好呢?SVM将会寻找可以区分两个类别并且能使间隔(margin)最大的划分超平面。比较好的划分超平面,样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。
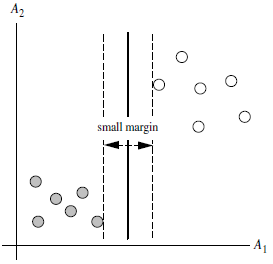
margin是什么?
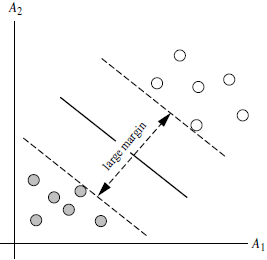
对于任意一个超平面,其两侧数据点都距离它有一个最小距离(垂直距离),这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin,虚线是由距离中央实线最近的两个点所确定出来的(也就是由支持向量决定)。但此时margin比较小,如果用第二种方式画,margin明显变大也更接近我们的目标。


支持向量(support vector)是什么?
从上图可以看出,虚线上的点到划分超平面的距离都是一样的,虚线穿过距离hyperplane最近的数据点,实际上就是这几个数据点共同确定了超平面的位置,因此被称作 “支持向量(support vectors)”,“支持向量机” 也是由此来的。
Support Vectors are defined as the data points, which are closest to the hyperplane and have some effect on its position. As these vectors are supporting the hyperplane, therefore named as Support Vectors.
一个hyperplane可由一个线性方程定义:\(w\cdot x + b = 0\),x为样本的特征向量,w是hyperplane的法向量,b是偏移。
SVM算法应用到多分类问题:
SVM can only perform binary classification (i.e., choose between two classes). However, there are various techniques to use for multi-class problems. Support Vector Machine for Multi-Class Problems To perform SVM on multi-class problems, we can create a binary classifier for each class of the data. For example, in a class of fruits, to perform multi-class classification, we can create a binary classifier for each fruit. For say, the "mango" class, there will be a binary classifier to predict if it IS a mango OR it is NOT a mango. The classifier with the highest score is chosen as the output of the SVM.
这是个小技巧,在面对多分类问题的时候,其实是为每一个分类,训练出一个是或不是的hyperplane,One-vs-Rest。
SVM算法应用与线性不可分的场景:
SVM for complex (Non Linearly Separable) SVM works very well without any modifications for linearly separable data.
什么是线性可分和线性不可分?
能够用一条直线对样本点进行分类的属于线性可区分(linear separable),否则为线性不可区分(linear inseparable)。
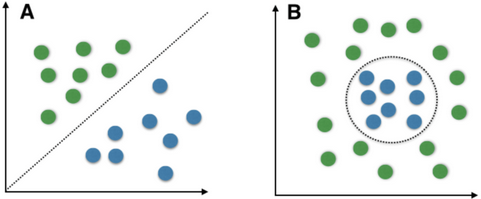
简单地从直觉上理解,上图A是线性可分的,用一个hyperplane就可将两类数据分开,而B是线性不可分的,没有任何一个hyperplane可以将这两类数据分开。
在线性不可分的情况下,数据集(样本集)在空间中对应的向量无法被一个超平面区分开,如何处理?利用一个非线性的映射把原数据集中的向量映射(transformation)到一个更高维度的空间中,然后在这个高维度的空间中,找一个超平面来根据线性可分的情况处理。
We use Kernelized SVM for non-linearly separable data. Say, we have some non-linearly separable data in one dimension. We can transform this data into two dimensions and the data will become linearly separable in two dimensions. This is done by mapping each 1-D data point to a corresponding 2-D ordered pair. So for any non-linearly separable data in any dimension, we can just map the data to a higher dimension and then make it linearly separable. This is a very powerful and general transformation.
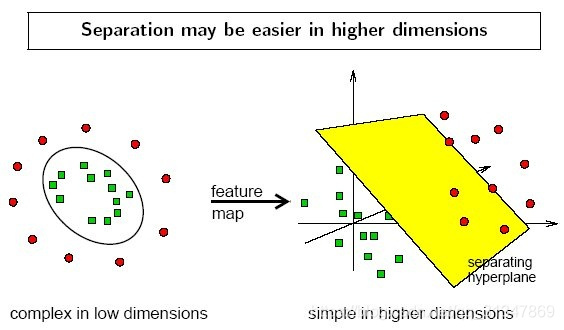
Kernelized SVM可以解决样本数据从低维到高维的映射问题,这种方法还提供了另一个好处,降低的算法的计算量。
在SVM算法中,转化为最优化问题时,求解的公式计算都是以内积(dot product)形式出现的,因为内积的算法复杂度(计算量)很大,所以我们利用核函数来取代计算非线性映射函数的内积。(是否可以这样理解,其实我们不太容易判断一堆数据是否线性可分,干脆全部采用核函数的方式,同时将数据映射到高维空间,也减少计算量)
A kernel is nothing but a measure of similarity between data points. The kernel function in a kernelized SVM tells you, that given two data points in the original feature space, what the similarity is between the points in the newly transformed feature space.
The SVM algorithm takes care of that by using a technique called the
kernel trick. The SVM kernel could be a function that takes low dimensional input space and transforms it into a better dimensional space, i.e., it converts non-separable problems to separable problems.
不同的任务,需要选择不同的核函数。
没有kernel的SVM也就是一个线性分类器,与LR(logistic regression)没有本质的差别,就连目标函数都很相似。线性分类器是指它的decision boundary是线性的,但训练数据并不一定能被线性区分开(linear speratable),这种情况经常被描述为“线性模型的表达或拟合能力不够”。
SVM算法特点:
Python生态scikit-learn库里有svm的实现:https://scikit-learn.org/stable/modules/svm.html#svm-classification
本文链接:https://cs.pynote.net/ag/ml/202210026/
-- EOF --
-- MORE --