自制对称加解密算法

密码学专业书籍总是警告：不要尝试自研加密算法......我还没有悟到......

在以前的某个项目中，使用过一个简单的加密解密方法，做个记录。

def cipherByte(abyte, pos=1):
    """Return a random big ordered uint32 which hide a byte in pos.
    pos cannot be zero because the returned uint32 would not be random
    enough in this case.
    """
    if pos not in (1,2,3):
        raise ValueError('pos value is not right.')
    b4 = b''
    while pos > 0:
        b4 += bytes([random.randint(0,255)])
        pos -= 1
    b4 += abyte
    while len(b4) < 4:
        b4 += bytes([random.randint(0,255)])
    return int.from_bytes(b4, 'big')


def decipherByte(uint32, pos=1):
    """Return the byte value which is in pos of a big ordered uint32.
    decipherByte is used in pair with cipherByte with the same pos value.
    byte value is 0 -- 255 in int.
    """
    if pos not in (1,2,3):
        raise ValueError('pos value is not right.')
    return uint32.to_bytes(4,'big')[pos]

对一个byte进行加密解密，将这个byte的内容，藏到一个uint32中去，解密的时候，再将这个byte从uint32中取出来。

这个简单的加密方法有个特点，对相同的byte加密，每次加密后得到结果都不一样，但解出来是一样的。此算法的关键，在于position！一串uint32数据，对应一串position ，这一串position数据就成了密钥，但由于每个position本身取值很有限，因此暴力破解也很容易。因此，不要透露加密方法，不要透露密钥，这两者和起来，成为了破解的关键。

凯撒密码

$ python3 -c 'import this'

Python标准lib中的this模块，只会打印出zen of python，这个模块中有一小段解密代码，用的就是凯撒密码，具体为rot13加密。

s = """Gur Mra bs Clguba, ol Gvz Crgref

Ornhgvshy vf orggre guna htyl.
Rkcyvpvg vf orggre guna vzcyvpvg.
Fvzcyr vf orggre guna pbzcyrk.
Pbzcyrk vf orggre guna pbzcyvpngrq.
Syng vf orggre guna arfgrq.
Fcnefr vf orggre guna qrafr.
Ernqnovyvgl pbhagf.
Fcrpvny pnfrf nera'g fcrpvny rabhtu gb oernx gur ehyrf.
Nygubhtu cenpgvpnyvgl orngf chevgl.
Reebef fubhyq arire cnff fvyragyl.
Hayrff rkcyvpvgyl fvyraprq.
Va gur snpr bs nzovthvgl, ershfr gur grzcgngvba gb thrff.
Gurer fubhyq or bar-- naq cersrenoyl bayl bar --boivbhf jnl gb qb vg.
Nygubhtu gung jnl znl abg or boivbhf ng svefg hayrff lbh'er Qhgpu.
Abj vf orggre guna arire.
Nygubhtu arire vf bsgra orggre guna *evtug* abj.
Vs gur vzcyrzragngvba vf uneq gb rkcynva, vg'f n onq vqrn.
Vs gur vzcyrzragngvba vf rnfl gb rkcynva, vg znl or n tbbq vqrn.
Anzrfcnprf ner bar ubaxvat terng vqrn -- yrg'f qb zber bs gubfr!"""

d = {}
for c in (65, 97):
    for i in range(26):
        d[chr(i+c)] = chr((i+13) % 26 + c)

print("".join([d.get(c, c) for c in s]))

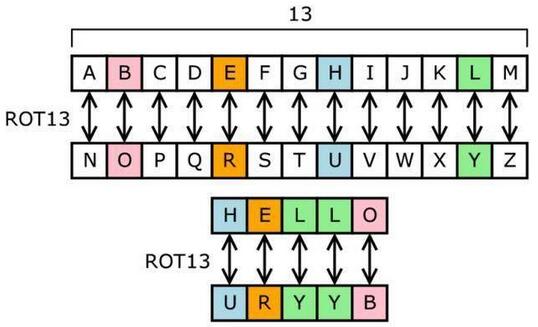
rot13就是凯撒密码的一种，每个字母变换为它后面的第13个字母。例如A变换为它后面的第13个字母N，所有字母变换关系如下图：

凯撒密码存在一个问题，即如果每次发送的是相同的字符串，加密后得到的也是相同的密文，比如在网络通信的时候。攻击者不用解密，直接使用这个相同的密文就可以发起攻击。

替换算法

前面的凯撒密码，实际上是一种替换算法，有规律的替换，秘钥很简单，rot13就是密钥。其实，还可以更复杂一些，用无规律的密码本来进行替换，就像谍战大片中的密码本一样，只要密码本能够保密，敌人就无法破解。

重排序（栅栏）

将待加密数据按一个固定的长度排成行，然后按列取，重排！

base64

不要单独使用bas64，这是基本上一眼就能通过密文看出加密算法的算法。

用XOR做mask

下面是个非常初级的掩码算法，使用base64的目的是为了把密文中的各种space符号去掉，在用tcp发送之前，可以在最后加上换行，方便收发：

import random

def cx(bmsg: bytes) -> bytes:
    m = random.randint(0,255)
    return base64.b64encode(bytes([m]+[i^m for i in bmsg]))

def dx(bmsg: bytes) -> bytes:
    bmsg = base64.b64decode(bmsg)
    return bytes([i^bmsg[0] for i in bmsg[1:]])

import random

def cx(bmsg: bytes) -> bytes:
    r = random.randint
    m = r(0,255)
    return base64.b64encode(bytes([m]+[i^m for i in bmsg])
                          + bytes([i^r(0,255) for i in range(m)]))

def dx(bmsg: bytes) -> bytes:
    bmsg = base64.b64decode(bmsg)
    return bytes([i^bmsg[0] for i in bmsg[1:len(bmsg)-bmsg[0]]])

>>> 0 ^ 0
0
>>> 1 ^ 0
1
>>> 0 ^ 1
1
>>> 1 ^ 1
0

多bit的XOR

门电路中的与们和或门，其输入都可以多于两个，这也很好理解。多个bit的与（AND），只要有一个bit为0，结果就是0；多个bit的或（OR），只要有一个bit为1，其结果就是1。

异或（XOR）运算也可以多bit同时进行：多个bit进行异或（XOR）的时候，奇数个1时，结果为1；偶数（含0）个1时，结果为0。

1遇到1变成0，1遇到0还是1，就像扑克牌比大小，只是需要注意，这个结论说明一个重要的细节：多个bit在XOR的时候，结果与计算顺序无关。这跟AND和OR的计算一样。

下面是python的演示，以上结论应该是可以用数学进行证明的。

>>> 1^0^1^0^1
1
>>> 1^0^1^0^1^0
1
>>> 1^1^1^0^0^0
1
>>> 0^0^0^1^1^1
1
>>> 1^1^0^0^1^0
1
>>> 0^0^1^1^0^1
1
>>>
>>>
>>>
>>> 0^0
0
>>> 0^0^0
0