-- TOC --
1973年,NSA向社会征集满足安全要求的加密算法。1973-1974年,IBM研发了DES加密算法。1974年,NSA开始了第二次征集,此后DES在1976年成为美国联邦标准。
DES算法:给定一个 64 位的明文和一个 64 位的密钥,输出一个 64 位的密文。对密文用相同的密钥解密。所谓64位的密钥,其实里面只有54位在起作用。剩余的位可以直接丢弃,或者当作奇偶校验位。DES 有一个非常不平凡的性质——加密与解密算法几乎一模一样。
整个DES算法可以分成两个部分:

$$\begin{aligned} L' &= R \\ R' &= L \oplus F(R, subkey)\end{aligned}$$
其中\(F\)函数(称为轮函数)是整个算法的核心,功能是:以一个子密钥,加密 32-bit 的信息。(DES算法内唯一执行XOR地方)
与加密流程有2处不同:
DES的安全性在很大程度上取决于 F 函数,也就是轮函数。那么 Feistel 函数是干了什么事呢?来看下面一张流程图:
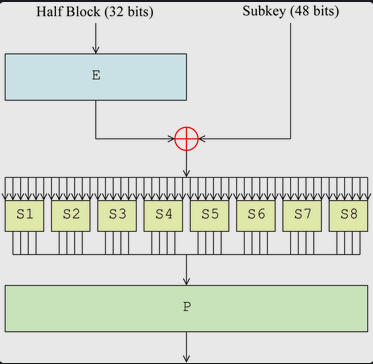
一个 32 位的块,经过一个扩张(Expand函数),变成 48 位,然后与子密钥异或!得到的 48 位的结果,将此结果分为 8 组,每一组是 6 位数据,丢进对应的 S 盒,输出 4 位信息。把这些输出收集起来,一共是 4*8 = 32 位,再做一次置换 (P置换),长度不变。
需要注意一点:这个 P 置换是精心设计的,使得这一轮同一个 S 盒 输出的四个 bit,在下一回合的扩张之后,交由四个不同的 S 盒去处理。
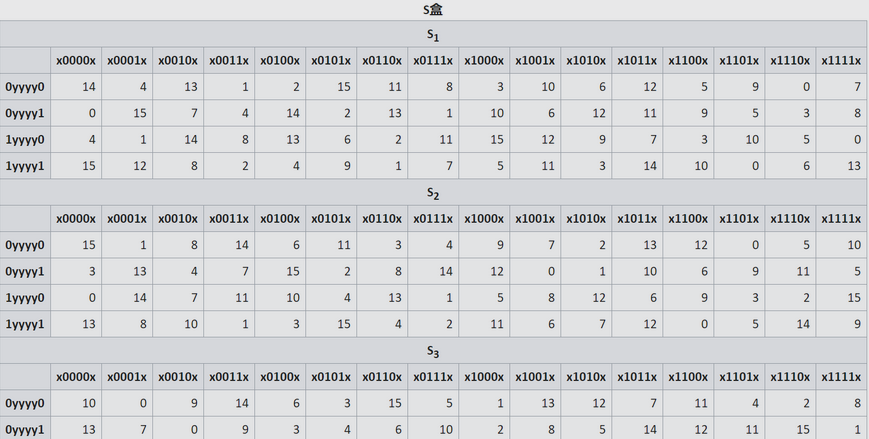
此图不完整,理解含义之后,代码中有完成的s盒。
扩张(E)之后的半块与子密钥异或,得到了 48 位结果,将此结果分成 8 个组,每组 6 位。然后第一组使用 S1 这张表进行变换,第二组使用 S2 进行变换……依次类推。现在我们假设第二组是 101100 ,来看它在 S盒变换之后会得到什么结果:
第二组,故查询 S2 表。1、末尾是0 ,故查询第三行(1yyyy0行)。0110 ,查表知结果是 13。1101 ,于是这就是输出。 from functools import reduce
def int2binlist(a, n):
assert 0<=n and a<(2**n)
return list(map(int,bin(a)[2:].rjust(n,'0')))
def binlist2int(a):
return reduce(lambda x,y: x*2+y, a)
# 选择置换1,输入 key 为长度为 64 的 0/1 数组
# 从64位输入密钥中选择56位,分为左右两个28位半密钥
def PC1(key):
assert len(key) == 64
pc1_l = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36]
pc1_r = [63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
return [key[x-1] for x in pc1_l], [key[x-1] for x in pc1_r]
# 选择置换2, 从56位的密钥中选取48位子密钥
def PC2(key):
assert len(key) == 56
pc2 = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32]
return [key[x-1] for x in pc2]
# 循环左移off位
def leftRotate(a, off):
return a[off:] + a[:off]
# 子密钥生成算法,由一个64位主密钥导出16个48位子密钥
def keyGen(key):
assert len(key) == 64
l, r = PC1(key)
off = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
k16 = []
for i in range(16):
l = leftRotate(l, off[i])
r = leftRotate(r, off[i])
k16.append(PC2(l + r))
return k16
# 初始置换
def IP(a):
ip = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
return [a[x-1] for x in ip]
# 最终置换
def FP(a):
fp = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
return [a[x-1] for x in fp]
# 扩张置换,将32位的数据扩展到48位
def E(a):
assert len(a) == 32
e = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
return [a[x-1] for x in e]
# P置换
def P(a):
assert len(a) == 32
p = [16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25]
return [a[x-1] for x in p]
# 异或
def binXor(a, b):
assert len(a) == len(b)
return [x^y for x,y in zip(a, b)]
S_box = [[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13],
[15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9],
[10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12],
[7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14],
[2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3],
[12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13],
[4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12],
[13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]
# S盒变换,输入48位,输出32位
def S(a):
assert len(a) == 48
a = [a[i*6:i*6+6] for i in range(8)]
res = []
for i in range(8):
p = a[i]
r = S_box[i][binlist2int([p[0], p[5], p[1], p[2], p[3], p[4]])]
res += int2binlist(r, 4)
assert len(res) == 32
return res
# F函数,用于处理一个半块
def Feistel(a, subKey):
assert len(a) == 32
assert len(subKey) == 48
return P(S(binXor(E(a),subKey)))
def goRound(l, r, subKey):
return r, binXor(l, Feistel(r, subKey))
def DES(plain, key, method):
subkeys = keyGen(int2binlist(key, 64))
if method == 'decrypt':
subkeys = subkeys[::-1]
m = IP(int2binlist(plain, 64))
l, r = m[:32], m[32:]
for i in range(16):
l, r = goRound(l, r, subkeys[i])
return binlist2int(FP(r + l))
print(hex(0x2973a7e54ec730a3))
print(hex(DES(0x11aabbccddeeff01, 0xcafababedeadbeaf, 'encrypt')))
print(hex(0x11aabbccddeeff01))
print(hex(DES(0x2973a7e54ec730a3, 0xcafababedeadbeaf, 'decrypt')))
DES提出的时候,由于 S 盒来历不明,以及传说 NSA 唆使 IBM 公司把有效密钥长度从 64 位减少到 56 位,DES 被怀疑有 NSA 留下的后门。直到上世纪 90 年代, “差分密码攻击”被公开提出,相关质疑终于消解 —— DES 的 S 盒,恰到好处地提供了对差分密码攻击的超强防御能力。而如果采用随机的 S 盒,抗差分密码攻击的能力则大大减弱。事实上,IBM 的研究员们早在 70 年代就已经发现了差分密码攻击方法,并针对此攻击方式特殊构建了 S 盒。出于国家安全的考虑,NSA 要求 IBM 保守秘密,于是差分密码攻击方法在二十余年后才得以重新被其他人发现。
本文链接:https://cs.pynote.net/se/jjm/202304162/
-- EOF --
-- MORE --