PCM和数字音频

Last Updated: 2023-05-22 09:52:13 Monday

-- TOC --

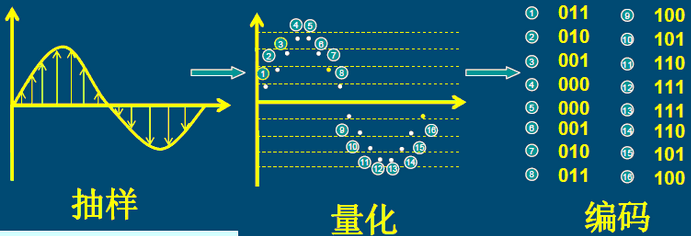
模拟信号的数字化方法：PCM。ADC就是模拟转数字，DAC就是数字转回模拟。

PCM是一种模拟信号的数字化方法，ADC（Analog to Digital Converter）芯片是实现这一方法的器件。

模拟信号是指随时间连续变化的物理量，将声音在磁带上记录成磁场强度的变化或在黑胶唱片上记录成沟槽大小的变化就是以模拟方式进行存储。数字信号则是离散的，计算机中的数据都以离散数字方式存储。

脉冲编码调制PCM（Pulse Code Modulation）是一种模拟信号的数字化方法。它是最常用、最简单的波形编码方式。

声音

声音三要素：

1. 音调，震动频率；
2. 音量，震动幅度；
3. 音色，谐波；

PCM原理

PCM实际上并没有"调制"的过程，而且也并没有脉冲出现，只因为PCM来源于PWM和PPM技术，所以也保留了"脉冲"二字。所以将脉冲编码调制（PCM）理解为一种模拟信号的数字化方法是最准确的。

PCM原理简单且容易理解，但现实中存在很多不同的PCM方案，比如不同的采样率，不同的量化方案等等。

采样率

采样率（采样频率）即每秒内进行采样的次数，单位是Hz。采样率越高，数字波形的形状就越接近原始模拟波形，声音的还原就越真实。

根据奈奎斯特－香农采样定理，只有采样频率高于原始模拟信号中最高频率的两倍时，才能把数字信号表示的模拟信号准确还原回去。例如，CD的采样率为每秒44100个采样，因此可重现最高为22050Hz的频率，此频率刚好超过人类的听力极限20000Hz。实际应用中，采样频率一般为信号最高频率的2.56～4倍。

以下是一些常见场景的数字音频采样率和采样位数：

narrowband，wideband这两个专业术语，指的就是采样率。

采样位数

采样位数（又称位宽，位深，bit-depth），字面意义就是采样值的二进制编码的位数。采样位数反应了采样系统对声音的辨析度，位数越高，对声音的记录就越精细，所以也称之为采样精度，采样深度。

采样位数的含义是用多少个bit来描述声音信号的强度，如上图的PCM编码的位数就是3bit，即有2^3 = 8个点。如果是8bit，就有2^8 = 256个点。

采样位数直接影响采集信号的信噪比和动态范围。较高的采样位数可提供更多可能的振幅值，产生更大的动态范围、更低的噪声基准和更高的保真度。

量化

量化过程是将采样信号变为离散时间和离散幅度的数字信号，量化过程又被分为线性量化和非线性量化。线性量化在整个量化范围内，量化间隔均相等。非线性量化采用不等的量化间隔。

声道（Sound Channel）

声道是指声音在录制或播放时，在不同空间位置采集或回放的，相互独立的音频信号。通俗的说，声道数就是录音时的麦克风数量，或是播放时的音响数量。声道数，也叫通道数，轨道数，音轨数。

常见的声道数有单声道（Mono），双声道（即立体声，Stereo），5.1声道，7.1声道等。这里的.1声道指的是低音声道SW（Subwoofer），即低音炮。

立体声，就是双声道...

音频编码

PCM（脉冲编码调制）是一种模拟信号的数字化方法，PCM编码就是这个方法中的数字音频编码方式。PCM编码是最原始的音频编码，其他编码都是在它基础上的再次编码。同视频一样，编码是为了压缩，音频编码也分有损和无损两种。

PCM文件是存储PCM编码音频的文件，是未经压缩的原始数字音频文件，通常称为PCM裸流/音频裸数据/raw data，常用文件扩展名是.pcm和.raw，通常它们是不能直接播放的。PCM裸流经过重新编码封装后，比如变为.wav格式，就可以正常播放了。

同视频一样，音频也有文件格式和编码格式的区别。

理论上说，任何数字音频都是无法完全还原模拟信号的。不过PCM编码是模拟信号转换为数字信号时的原始编码，它代表着数字音频的最佳保真水平，所以PCM编码就约定俗成为无损编码。

音频比特率的计算

音频比特率 = 采样率×采样位深×通道数

采样频率44.1KHz，采样位数16bit，立体声的PCM音频。这段音频的比特率就是44100*16*2 = 1411.2Kbps。

DPCM

DPCM（Differential Pulse Code Modulation），差分脉冲编码调

PCM是不压缩的，通常数据量比较大，存储和通讯都必需付出比较大的代价，早期的通讯也无法传输那么大的数据量，所以就要想办法把数据压缩一下，以减少带宽和存储的压力。

假设我们以8kHz的采样率，16bit量化编码，则1秒的数据量为8000 * 16 = 128000 bit = 16000 byte 。

一般音频信息都是比较连续的，不会突然很高或者突然很低，两点之间差值不会太大，所以这个差值只需要很少的几个位（比如4bit）即可表示。这样，我们只需要知道前一个点的值，又知道它与下一个点的差值，就可以计算得到下一个点了。

这个差值就是所谓的Differential ，将PCM数据转成DPCM数据，数据里会小很多，如上面所说的用4bit的表示差值，则1秒的（8kHz采样率，16bit量化编码）PCM数据转成DPCM则只需要大约32000bit, 压缩比大约4:1。

ADPCM

ADPCM(Adaptive Differential Pulse Code Modulation)、自适应差分脉冲编码调

音频信号虽然是比较连续性的，有些差值比较小，有些差值比较大，如果差值比较大有可能用4bit表示不了，如果增大表示差值的位数（例如8bit\16bit）是可以解决这个问题，但就导致数据量变大，没起到压缩的目的，而且这种差值比较大的只是少数，大部分还是差值比较小的。

为了解决这个问题，前辈们就想出了ADPCM，定义一个因子，用差值除以因子的值来表示两点之差，如果两点之间差值比较大，则因子也比较大。通过因子引入，可以使得DPCM编码自动适应差值比较大的数据。

ADPCM算法并没用固定标准，最经典的就是IMA ADPCM

G.711

G.711是国际电信联盟ITU-T定制出来的一套语音压缩标准，它代表了对数PCM（logarithmic pulse-code modulation）抽样标准，是主流的波形声音编解码标准，主要用于电话。

G.711 标准下主要有两种压缩算法。

• u-law algorithm （又称u-law, ulaw, mu-law），主要运用于北美和日本。
• A-law algorithm，主要运用于欧洲和世界其他地区。特别设计用来方便计算机处理的。

G.711将14bit（uLaw）或者13bit（aLaw）采样的PCM数据编码成8bit的数据流，播放的时候在将此8bit的数据还原成14bit或者13bit进行播放，G711是波形编解码算法，就是每1个sample对应1个编码，所以压缩比固定为：

• 8/14 = 57% (uLaw)
• 8/13 = 62% (aLaw)

G.711的采样率为8KHz，刚好适合64Kbps的古老的语音通道。

我理解所谓对数PCM，就是高特别高和特别低的声音区域，采用比较平缓的编码，即在这两个区域的实际bit-depth较小，图形上看像对数函数的图形。

Wave文件格式

wav文件格式，是微软开发的一种文件格式规范。wave文件其实就是在PCM数据前面加了一个头，让播放器可以用正确的参数去解析后面的PCM码流。

更详细的参考网页：http://www-mmsp.ece.mcgill.ca/Documents/AudioFormats/WAVE/WAVE.html

• wave文件前4个byte是magic：RIFF（ Resource Interchange File Format）；
• 然后是4个byte的size，这个size去掉了前面8个byte，因此+8就是整个文件的size；
• 然后是4个byte，WAVE；

>>> f = open('Alarm01.wav', 'rb')
>>> f.read(4)
b'RIFF'
>>> int.from_bytes(f.read(4), 'little')
491508  # +8 is file size
>>> f.read(4)
b'WAVE'

上面的部分叫做RIFF chunk。

后面是fmt chunk的数据：

• 4 bytes，b'fmt\0x20'；
• 4 bytes， size，这部分后面的大小,我见过16，也出现过40;
• 2 bytes， audio format，

>>> f.read(4)
b'fmt '
>>> int.from_bytes(f.read(4), 'little')
16
>>> int.from_bytes(f.read(2), 'little') 
1

• 2 bytes，number of channels；
• 4 bytes，sample rates，采样率；
• 4 bytes，byte rate；
• 2 bytes，block align；
• 2 bytes，bits per sample；

>>> int.from_bytes(f.read(2), 'little')
2
>>> int.from_bytes(f.read(4), 'little') 
22050
>>> int.from_bytes(f.read(4), 'little')
88200
>>> int.from_bytes(f.read(2), 'little') 
4
>>> int.from_bytes(f.read(2), 'little')
16

以上数据的解释：22050的采样率，bit-depth 16bit，即2 bytes，双声道，因此每次采样有4个bytes，4个bytes为一个block，byte rate就等于22050*4=88200。

最后是data chunk部分。

• 4 bytes，data
• 4 bytes， data size，后面data的size；

>>> f.read(4)
b'data'
>>> int.from_bytes(f.read(4), 'little') 
491472
>> 491472 // 4
122868  # frame number
>> f.close()

arecord命令的manpage，可以看到有非常的不同的数据格式。但似乎wave文件默认其中保存的PCM数据，都是signed little-endian格式！

-f --format=FORMAT Sample format Recognized sample formats are: S8 U8 S16_LE S16_BE U16_LE U16_BE S24_LE S24_BE U24_LE U24_BE S32_LE S32_BE U32_LE U32_BE FLOAT_LE FLOAT_BE FLOAT64_LE FLOAT64_BE IEC958_SUBFRAME_LE IEC958_SUBFRAME_BE MU_LAW A_LAW IMA_ADPCM MPEG GSM SPECIAL S24_3LE S24_3BE U24_3LE U24_3BE S20_3LE S20_3BE U20_3LE U20_3BE S18_3LE S18_3BE U18_3LE Some of these may not be available on selected hardware The available format shortcuts are: -f cd (16 bit little endian, 44100, stereo) [-f S16_LE -c2 -r44100] -f cdr (16 bit big endian, 44100, stereo) [-f S16_BE -c2 -r44100] -f dat (16 bit little endian, 48000, stereo) [-f S16_LE -c2 -r48000] If no format is given U8 is used.

PCM存储格式大体分为两种Planner和Packed 我们以双声道为例，L表示左声道，R表示右声道，如下为两种格式的存储方式：

Planner：

LLLLLLLL......RRRRRRRR......

Packed：

LRLRLRLR.......

Python的wave模块

Python标准库中提供了一个wave模块，用来读写标准wave文件。

下面展示wave模块读相关接口，用于前面一节相同的文件，相关数据可以对比参考学习：

>>> import wave
>>> rf = wave.open('Alarm01.wav', 'rb')
>>> rf.getnchannels()
2
>>> rf.getsampwidth()
2
>>> rf.getframerate()
22050
>>> rf.getnframes()
122868
>>> rf.getparams()
_wave_params(nchannels=2, sampwidth=2, framerate=22050, nframes=122868, comptype='NONE', compname='not compressed')
>>> rf.readframes(1)
b'\x00\x00\x00\x00'
>>> rf.readframes(4) 
b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'
>>> rf.tell()
5
>>> rf.close()

一个不兼容的case

我用ffmpeg将一个mp3文件转成wav，在wav文件的fmt部分，audio format被ffmpeg写成了65534，不再是1。这个wav文件用Python的wave模块打不开，直接报错。不知道什么情况？

为了继续使用Python的wave模块，我将wave.py拷贝到工作目录下，直接修改了WAVE_FORMAT_PCM这个变量的值。

单麦克风录音

单麦克风只能产生单音轨，即一个channel。

用arecord录音，如果只有一个麦克，但是设置的channel大于1，也能够成功，只是输出的数据只有一个channel有数据，其它channel没有数据。

有些录音软件在单麦克的情况下，也能录制stereo，这是软件自己复制了一份数据到另一个声道导致的，这种软件一般都是非专业的软件。

如果考虑音频数据的网络传输，单麦克就得是单声道数据，不要无故增大传输的数据量，要做处理也是在接收端进行。

音频数据的latency

Within the audio interface is an area referred to as the "hardware buffer". As an audio signal arrives from the outside world, the interface converts it into a stream of bits usable by the computer and stores it in the part hardware buffer used to send data to the computer. When it has collected enough data in the hardware buffer, the interface interrupts the computer to tell it that it has data ready for it.

A similar process happens in reverse for data being sent from the computer to the outside world. The interface interrupts the computer to tell it that there is space in the hardware buffer, and the computer proceeds to store data there. The interface later converts these bits into whatever form is needed to deliver it to the outside world, and delivers it. It is very important to understand that the interface uses this buffer as a "circular buffer". When it gets to the end of the buffer, it continues by wrapping around to the start.

For this process to work correctly, there are a number of variables that need to be configured. They include:

• what format should the interface use when converting between the bitstream used by the computer and the signal used in the outside world?
• at what rate should samples be moved between the interface and the computer?
• how much data (and/or space) should there be before the device interrupts the computer?
• how big should the hardware buffer be?

The first two questions are fundamental in governing the quality of the audio data. The second two questions affect the "latency" of the audio signal. This term refers to the delay between

• data arriving at the audio interface from the outside world, and it being available to the computer ("input latency")
• data being delivered by the computer, and it being delivered to the outside world ("output latency")

Both of these are very important for many kinds of audio software, though some programs do not need be concerned with such matters.

音量控制

操作系统中的音量控制，从0到100，（正确的处理方式）是非线性的。

根据人耳的声心理学的研究，人耳对声音大小的感知程度并不是线性的，而是呈对数关系，对数形式的单位是dB。

数字音频领域，通常0dB代表最大音量，0dB意味着不对数据进行任何的变换处理，输出等于输入。（Windows系统中的麦克风驱动，接收到的用户界面对麦克风音量的调节信号，100时收到0，0时收到一个很大的负数，-6291456）

对声音波形振幅的调整，就可以实现调整音量。PCM=0时表示没有声音，PCM数据的绝对值越大，即振幅越大，音量也越大。（wave文件中的PCM数据，signed and little-endian，可直接乘上一个百分比后取整）

下面的代码，读取一个wave文件的前2000个frame，作图：

import numpy as np
import matplotlib.pyplot as plt 
import wave

rf = wave.open('liker.wav', 'rb')
frame_num = rf.getnframes()
frame_num = 2000
x = [i for i in range(frame_num)]
y1 = [int.from_bytes(rf.readframes(1),'little',signed=True)
         for i in range(frame_num)]
y2 = [int(v*0.5) for v in y1]

fig = plt.figure('graph of wave')
ax1 = fig.add_subplot(121)
ax1.plot(x,y1,linewidth=0.2)
ax2 = fig.add_subplot(122)
ax2.plot(x,y2,linewidth=0.2)
plt.show()

输出图：

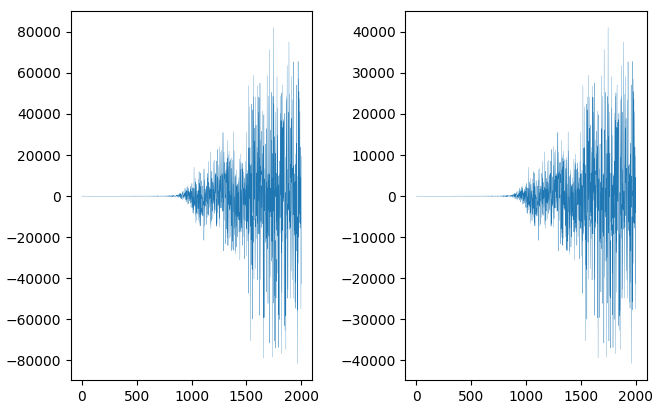
注意纵轴范围的变化，以及不变的wave pattern！

Windows麦克风驱动收到的volume值（type is int32），经过了normalization：

肉眼就能看出，靠近音量100的区域，斜率很大，靠近音量0的区域，斜率很小。

驱动内正规化的代码:

// Default volume settings.
#define VOLUME_STEPPING_DELTA       0x8000
#define VOLUME_SIGNED_MAXIMUM       0x00000000
#define VOLUME_SIGNED_MINIMUM       (-96 * 0x10000)

// Default peak meter settings
#define PEAKMETER_STEPPING_DELTA    0x1000
#define PEAKMETER_SIGNED_MAXIMUM    LONG_MAX
#define PEAKMETER_SIGNED_MINIMUM    LONG_MIN

#define VALUE_NORMALIZE_P(v, step) \
    ((((v) + (step)/2) / (step)) * (step))

#define VALUE_NORMALIZE(v, step) \
    ((v) > 0 ? VALUE_NORMALIZE_P((v), (step)) : -(VALUE_NORMALIZE_P(-(v), (step))))

#define VALUE_NORMALIZE_IN_RANGE_EX(v, min, max, step) \
    ((v) > (max) ? (max) : \
     (v) < (min) ? (min) : \
     VALUE_NORMALIZE((v), (step)))

// to normalize volume values.
#define VOLUME_NORMALIZE_IN_RANGE(v) \
    VALUE_NORMALIZE_IN_RANGE_EX((v), VOLUME_SIGNED_MINIMUM, VOLUME_SIGNED_MAXIMUM, VOLUME_STEPPING_DELTA)

构建非线性对应关系

从驱动内部保存的经过正规化后的值，到0 -- 1之间。

Windows的simpleaudiosample demo之所有没有使用获取到的正规化后的音量数据，可能的一个原因是，在驱动内，对每个frame数据进行计算（每10ms计算一次最新的百分比，每个frame计算一次浮点数乘法后取整），消耗可能有点大。一般这个计算，都是麦克风驱动硬件完成。

尝试用6次多项式进行拟合，失败，拟合出来的曲线，在点与点之间的空间，存在剧烈波动。

Windows驱动内可以做浮点数计算，但需要调用KeSaveFloatingPointState。

测试了浮点数乘法和整数乘法，浮点数乘法比整数乘法慢一点点，但这点速度，在麦克风驱动内部，应该是可以接受的。

#include <stdio.h>
#include <time.h>


int main(void) {
    unsigned long count = 1e9;
    long int c;
    printf("CLOCKS_PER_SEC = %d\n", CLOCKS_PER_SEC);
    printf("count = %lu\n", count);

    clock_t tic = clock();
    for (unsigned long i=0; i<count; ++i)
        c = i * 0.57f;
    clock_t toc = clock();
    unsigned long ticks1 = toc - tic;
    printf("float-time: %lu %.3fs\n", ticks1, ((float)ticks1)/CLOCKS_PER_SEC);

    tic = clock();
    for (unsigned long i=0; i<count; ++i)
        c = i * 57;
    toc = clock();
    unsigned long ticks2 = toc - tic;
    printf("  int-time: %lu %.3fs\n", ticks2, ((float)ticks2)/CLOCKS_PER_SEC);

    printf("diff-ticks: %lu\n", ticks1-ticks2);
    printf("per-count(ns): %.3fns\n", ((float)(ticks1-ticks2)*1000)/count);

    return 0;
}

分贝的计算公式：\(dB=20\cdot\log_{10}(\frac{A1}{A2})\)

当A1==A2的时候，0分贝，表示与输入音量相同。

结合这条拟合曲线，符合指数函数关系，通过尝试和测试发现，从normalization后的值到振幅的计算公式：

>>> zhenfu = pow(2, (-steps)/20)

曲线如下：

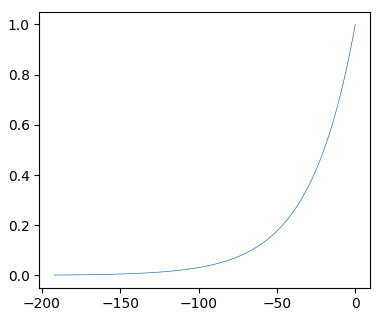
很完美！

本文链接：https://cs.pynote.net/ag/202207081/

-- EOF --

-- MORE --

• 如何计算CRC
• 并归排序（Merge Sort）
• 有头节点的链表（Linked List）实现
• 支持向量机SVM算法
• 位运算的妙用和坑
• 使用ffmpeg
• 霍夫曼（Huffman）压缩编码算法
• 寻找质数（prime number）

CS笔记 Since 2021.9
Powered by Python & Markdown