Last Updated: 2024-03-20 08:32:54 Wednesday
-- TOC --
假设你去超时买东西,不用微信,而是用传统的纸币,收银员要给你找零钱,只有5元,2元和1元的纸币,要找给你7元,每种面值的零钱无限量供应,一共有多少种不同的零钱组合方式找给你。注意:每种面值的零钱无限量供应!
答案如下:
7 = 1*7
7 = 2*3 + 1
7 = 2*2 + 1*3
7 = 2 + 1*5
7 = 5 + 2
7 = 5 + 1*2
用1元,2元和5元的纸币,组合成7元钱,一共有6种组合。
由于有1元的存在,一定可以找零,所以问题是有多少种不同的找零方式!
现在我们写一个函数来计算组合数:
def make_change(amount: int, coins: tuple[int]) -> int:
if amount == 0:
return 1
if amount < 0 or not coins:
return 0
i = make_change(amount-coins[0], coins)
j = make_change(amount, coins[1:])
return i+j
assert make_change(0,(5,2,1)) == 1
assert make_change(1,(5,2,1)) == 1
assert make_change(2,(5,2,1)) == 2
assert make_change(3,(5,2,1)) == 2
assert make_change(4,(5,2,1)) == 3
assert make_change(5,(5,2,1)) == 4
assert make_change(6,(5,2,1)) == 5
assert make_change(7,(5,2,1)) == 6
将找零问题划分成两个子问题:
最后把这两个子问题的结果相加。这两个子问题,绝对不会重合!
复杂度:
$$T(n,a)=T(n,a-c)+T(n-1,a)+1$$
现在我们将此问题更进一步,不是计算组合数量,而是把每一种具体的组合找出来,实现如下:
def make_change_d(amount: int, coins: tuple[int]) -> list[tuple[int,...]]:
if amount == 0:
return [()]
if amount < 0 or not coins:
return []
i = [z+(coins[0],) for z in make_change_d(amount-coins[0],coins)]
j = make_change_d(amount, coins[1:])
return i+j
assert len(make_change_d(0,(5,2,1))) == 1
assert len(make_change_d(1,(5,2,1))) == 1
assert len(make_change_d(2,(5,2,1))) == 2
assert len(make_change_d(3,(5,2,1))) == 2
assert len(make_change_d(4,(5,2,1))) == 3
assert len(make_change_d(5,(5,2,1))) == 4
assert len(make_change_d(6,(5,2,1))) == 5
assert len(make_change_d(7,(5,2,1))) == 6
from pprint import pprint
print('7:')
pprint(make_change_d(7,(5,2,1)))
print('10:')
pprint(make_change_d(10,(5,2,1)))
[()]时,表示找到了一个组合,此时会在调用层加上刚使用的那个coin[]时,表示这条路不通,返回上层后,listcomp不会有任何效果,i为空,加法也没效果输出:
7:
[(2, 5),
(1, 1, 5),
(1, 2, 2, 2),
(1, 1, 1, 2, 2),
(1, 1, 1, 1, 1, 2),
(1, 1, 1, 1, 1, 1, 1)]
10:
[(5, 5),
(1, 2, 2, 5),
(1, 1, 1, 2, 5),
(1, 1, 1, 1, 1, 5),
(2, 2, 2, 2, 2),
(1, 1, 2, 2, 2, 2),
(1, 1, 1, 1, 2, 2, 2),
(1, 1, 1, 1, 1, 1, 2, 2),
(1, 1, 1, 1, 1, 1, 1, 1, 2),
(1, 1, 1, 1, 1, 1, 1, 1, 1, 1)]
上述递归算法非常慢,Big-Oh为\(O(2^N)\),如果采用DP思路,将计算过程中的子问题的结果记录下来,在后续计算中直接使用,同样是递归,速度变得非常快!
result = {}
def make_change_dp_recursive(amount: int, coins: tuple[int]) -> int:
global result
if amount == 0:
return 1
if amount < 0 or not coins:
return 0
k = (amount-coins[0], coins)
try:
i = result[k]
except KeyError:
i = result[k] = make_change_dp_recursive(*k)
k = (amount, coins[1:])
try:
j = result[k]
except KeyError:
j = result[k] = make_change_dp_recursive(*k)
return i+j
直接取曾经计算过的子问题的结果,不再重复计算。如果计算(210,(5,2,1)),改进后的算法要快超过100倍!
run (210, (5, 2, 1)) with number = 200
make_change return: 2290
make_change_dp_recursive return: 2290
make_change average cpu time: 0.0429869594
make_change_dp_recursive average cpu time: 0.00041894424499999694
boost: 102.60782887708676
改进后的算法,Big-Oh是\(O(M\times N)\),M是amount的值大小,N是硬币种类的数量,因为每个子问题,只需要计算一次,后面再遇到,就是直接取值!\(M\times N\)就是所有子问题的数量。
下面是在make_change_dp_recursive基础上改出来的计算出所有组合的代码:
res = {}
def make_change_dp_recursive_d(amount: int, coins: tuple[int]) -> list[tuple[int,...]]:
global res
if amount == 0:
return [()]
if amount < 0 or not coins:
return []
k = (amount, coins)
try:
i = res[k]
except KeyError:
i = res[k] = [z+(coins[0],)
for z in make_change_dp_recursive_d(amount-coins[0],coins)]
k = (amount, coins[1:])
try:
j = res[k]
except KeyError:
j = res[k] = make_change_dp_recursive_d(*k)
return i+j
很多DP问题,都可以使用自底向上的循环的方式,一层层计算子问题,最后得到问题的解。找零问题也可以使用这个思路,代码如下:
def make_change_loop(amount: int, coins: tuple[int]) -> int:
w = [0] * (amount+1) # faster than listcomp
w[0] = 1
for c in coins:
for i in range(c, amount+1):
w[i] += w[i-c]
return w[-1]
assert make_change_loop(0,(5,2,1)) == make_change(0,(5,2,1))
assert make_change_loop(1,(5,2,1)) == make_change(1,(5,2,1))
assert make_change_loop(2,(5,2,1)) == make_change(2,(5,2,1))
assert make_change_loop(3,(5,2,1)) == make_change(3,(5,2,1))
assert make_change_loop(4,(5,2,1)) == make_change(4,(5,2,1))
assert make_change_loop(5,(5,2,1)) == make_change(5,(5,2,1))
assert make_change_loop(6,(5,2,1)) == make_change(6,(5,2,1))
assert make_change_loop(7,(5,2,1)) == make_change(7,(5,2,1))
w[0] = 1,目标是0时,有1种方法。w[i] += w[i-c],在w[i-c]的基础上,用一个c,就可得到w[i]。性能比较,结果比递归方案要快接近1000倍:
run (210, (5, 2, 1)) with number = 200
make_change return: 2290
make_change_loop return: 2290
make_change average cpu time: 0.04304871445
make_change_loop average cpu time: 4.425439500000294e-05
boost: 972.755687881331
DP循环方案是最快的!Sum越大,快的倍数越大!
下面是用DP循环的方式,计算所有的具体组合:
def make_change_loop_d(amount: int, coins: tuple[int]) -> list[tuple[int,...]]:
w = [[] for i in range(amount+1)] # cannot use [[]]*N
w[0].append(())
for c in coins:
for i in range(c, amount+1):
w[i] += [z+(c,) for z in w[i-c]]
return w[-1]
空间复杂度不够友好。但如果计算过程中,只是记录少量信息,最后需要回溯才能找出所有具体组合。很多DP问题满足条件的解都不止一个,找出所有的解也挺有挑战的。
单纯的递归方案有3个问题:
>>> import sys
>>> sys.setrecursionlimit(100)
>>> sys.getrecursionlimit()
100
>>> make_change(96,(5,2,1))
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "/home/xinlin/test/tt.py", line 7, in make_change
j = make_change(amount, coins[1:])
File "/home/xinlin/test/tt.py", line 7, in make_change
j = make_change(amount, coins[1:])
File "/home/xinlin/test/tt.py", line 6, in make_change
i = make_change(amount-coins[0], coins)
File "/home/xinlin/test/tt.py", line 6, in make_change
i = make_change(amount-coins[0], coins)
File "/home/xinlin/test/tt.py", line 6, in make_change
i = make_change(amount-coins[0], coins)
[Previous line repeated 93 more times]
File "/home/xinlin/test/tt.py", line 2, in make_change
if amount == 0:
RecursionError: maximum recursion depth exceeded in comparison
DP递归方案稍微好一点,但用处还是不大,虽然由于直接取子问题的值可以缓解递归深度的问题,但是并不能从更本上解决此问题,递归深度的问题,与输入密切相关:
>>> make_change_dp_recursive(96,(5,2,1))
500
>>> make_change_dp_recursive(96,(1,2,5))
...
RecursionError: maximum recursion depth exceeded in comparison
应该使用DP循环方案,它最快,而且没有递归深度问题。
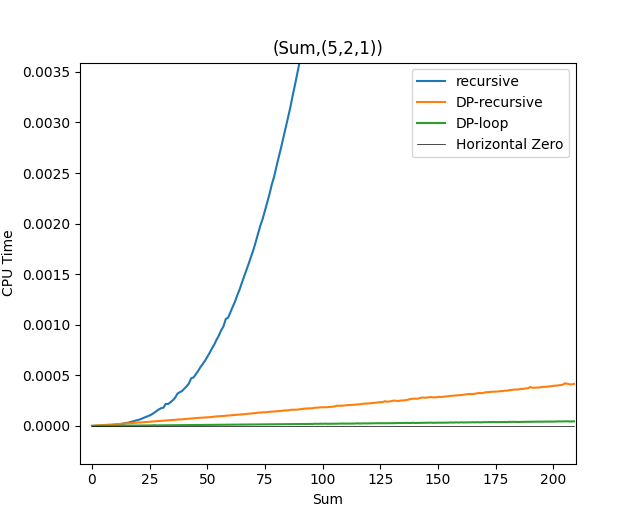
最后,上一张性能测试比较的图片:

本文链接:https://cs.pynote.net/ag/dp/202307131/
-- EOF --
-- MORE --