LeetCode第887题，高楼扔鸡蛋（通用版）

k个鸡蛋，n层高楼，通过扔鸡蛋的方式来判断到底从哪一层楼开始，鸡蛋broken。此题不是求解鸡蛋开始broken的楼层数，而是minimum number of drops with certainty。要certainty，这句话有点难理解！怎么样才能得到certainty？在能够保证certainty的前提下，最小的drop次数，对应的是best case，还是worst case？

Example 1:
Input: k = 1, n = 2
Output: 2
Explanation: 
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.

Example 2:
Input: k = 2, n = 6
Output: 3

Example 3:
Input: k = 3, n = 14
Output: 4

举个例子：k=2，n=6时，最少需要3次drop，就可以确定x楼层（鸡蛋开始broken的楼层），这是怎么来的？

6
5  <-- (2)
4
3  <-- (1)
2
1

我们的目标是，用2个鸡蛋，最少的drop数，确定能找到6层楼的x楼层，不同的运气导致x的不同，我们只需要能够确定x，不关心x的具体值，只要求drop数量最少。

第1次drop在3楼，为什么是3楼？因为如果鸡蛋broken，剩下1个鸡蛋，测试1楼和2楼，一共测试3次找到x。如果第1次不选择3楼，比如4楼，如果鸡蛋broken，剩下的1个鸡蛋，要确定找到x，最多需要4次drop，此时，少于4次都可能导致没有certainty，在只有1个鸡蛋时，我们处理的是worst case。要确定找到x，就是当只剩下1个鸡蛋的时候，只能从底向上，一层层测试，确定找到的drop次数，就是到达上面那个broken楼层或顶层的数量。这个确定的数量，是只剩1个鸡蛋时的最大值，worst case。如果第1次没有broken，第2次drop就在5楼，为什么不是6楼？如果第2次drop在6楼，鸡蛋broken，剩下一个鸡蛋，要确定6楼的情况，最多还需要2次drop，就是4次，不是最小值。不管在5楼的第2次drop是否broken，都还只需要1次drop，就可以在6层高的楼中，确定找到x楼层。因此，最少是3次！

可以看出，3次是一个均衡值，是不管鸡蛋broken与否，这个值都能够达到certainty的均衡的最小值！

不管x是具体哪一层，在只有2个鸡蛋时，最佳策略需要3次drop，就能确定x！最佳策略就是drop次数最小的策略，本题求解最佳策略的drop次数，但不要求次策略的具体内容，也不关心3次drop鸡蛋broken的情况。

递归（TLE）

如果只有一个鸡蛋，那么我们只有一个strategy，就是从低往高一层层的测试，要么鸡蛋broken，要么试完所有楼层。worst case就是后者，试完所有楼层，不管最后一次测试鸡蛋是否broken。

每当我们选择一个楼层i进行drop时，有两个结果，要么鸡蛋broken，此时只需要继续测试i以下的楼层，要么鸡蛋没有broken，此时只需要继续测试i以上的楼层。每一次选择，问题空间都会被切分乘两不分，但如何确定在哪个楼层进行切分，这样的策略，没有明显的答案。通过递归遍历所有的选择，选择minimum。

class Solution:    
    def superEggDrop(self, k: int, n: int) -> int:
        if k==1 or n==0:
            return n
        drop = n
        for i in range(1,n+1):
            maxdrop = 1 + max(self.superEggDrop(k-1,i-1),
                              self.superEggDrop(k,n-i))
            if maxdrop < drop:
                drop = maxdrop
        return drop

Dynamic Programming（TLE）

递归是超级慢的.....每一次楼层的选择，都将问题划分成了两个subproblem，递归计算直到k等于1或n等于0。由于我们只关注需要测试的楼层高度，而忽略具体是第几层，此时这些subproblem在递归过程中，就存在重叠，这就给Dynamic Programming提供了机会，去掉这些重复计算。

class Solution:    
    def _egg_drop(self, k, n):
        if (k,n) in self.sub:
            return self.sub[k,n]
        drop = n
        for i in range(1,n+1):
            maxdrop = 1 + max(self._egg_drop(k-1,i-1),
                              self._egg_drop(k,n-i))
            if drop > maxdrop:
                drop = maxdrop
        self.sub[k,n] = drop
        return drop

    def superEggDrop(self, k: int, n: int) -> int:
        self.sub = {(i,0):0 for i in range(1,k+1)}
        self.sub |= {(1,i):i for i in range(1,n+1)}
        return self._egg_drop(k,n)

这个DP版本的时间复杂度为：\(O(kn^2)\)。子问题的数量为\(kn\)，每个子问题内有一个for循环。

DP + Binary Search

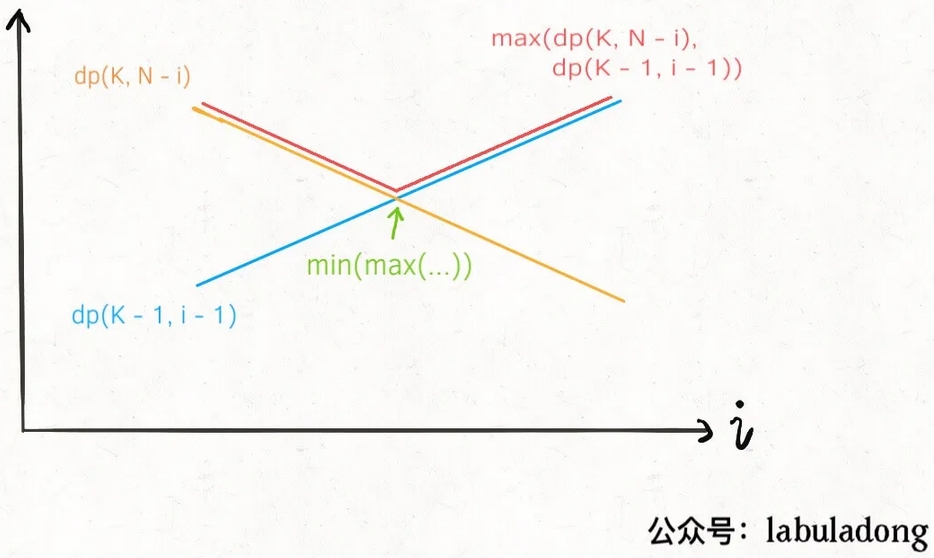
楼层数越高，在k不变的情况下，尝试的次数必然越多。i从1递增到n的过程，两个递归调用的返回值分别呈现单调递减和单调递增的特性。可用下图来表示（图片来自https://zhuanlan.zhihu.com/p/92288604）：

from math import ceil, sqrt

class Solution:    
    def _egg_drop_bsearch(self, k, n):
        if (k,n) in self.sub:
            return self.sub[k,n]
        drop = n
        lo = 1
        hi = n
        while lo <= hi:
            mi = (lo+hi) // 2
            broken = self._egg_drop_bsearch(k-1,mi-1)
            intact = self._egg_drop_bsearch(k,n-mi)
            if broken == intact:
                drop = min(drop, intact+1)
                break
            if broken < intact:
                lo = mi + 1
                drop = min(drop, intact+1)
            else:
                hi = mi - 1
                drop = min(drop, broken+1)
        self.sub[k,n] = drop
        return drop

    def superEggDrop(self, k: int, n: int) -> int:
        self.sub = {(i,0):0 for i in range(1,k+1)}
        self.sub |= {(1,i):i for i in range(1,n+1)}
        self.sub |= {(2,i):ceil(sqrt(i*2+0.25)-0.5) for i in range(1,n+1)}
        return self._egg_drop_bsearch(k,n)

DP（Bottom-Up）

从底向上逆向DP是很有挑战的，很多时候需要逆向思维，反过来想。前面的思路，都是在正向寻找k个鸡蛋在面对n层楼时，找到确定broken楼层的最小drop次数。反过来呢？k个鸡蛋，尝试m次，就能够确定找到broken楼层位置的最高楼层数n！

class Solution:    
    def superEggDrop(self, k: int, n: int) -> int:
        sub = [[0]*(n+1) for _ in range(k+1)]
        i = 0
        while sub[k][i] < n:
            i += 1
            for j in range(1,k+1):
                sub[j][i] = sub[j-1][i-1] + sub[j][i-1] + 1
        return i

LeetCode第887题，高楼扔鸡蛋（通用版）

题目分析

递归（TLE）

Dynamic Programming（TLE）

DP + Binary Search

DP（Bottom-Up）