Last Updated: 2023-10-25 12:37:04 Wednesday
-- TOC --
完成了LeetCode的两数和,三数和,以及四数和这三道题,我觉得是时候好好总结一下了!
理论上最快的排序算法,需要\(O(N\cdot\log{N})\)的时间复杂度,后面再跟Two Pointer的\(O(N)\),排序反而成了影响性能的关键了。因此,此时最快的算法,应该是遍历的同时建立Hashtable并查找。
理论上Hashtable的查找是\(O(N)\),因为这是考虑到了最坏的情况。现实中,我还是倾向于认为查找Hashtable是\(O(1)\),因为有各种手段来调整Hashtable的数据分布,控制碰撞的概率,使其保持在\(O(1)\)状态,如果做不到,会考虑放弃使用Hashtable。
此时,先做个排序是很有价值的,因为后面的每一次循环,都是在已排好序的结果上计算。一次排序,终身享受!
现实总是比理论要更加复杂。比如:
先对输入进行统计,如Python的Counter,此时就可以分情况处理,比如在计算3数和时,有无3个数一样的情况,有无2个数一样的情况,最后处理所有数都不一样的情况。而排序的结果,一定是不带重复数据的(有重复数据的情况,前面分情况已经处理掉了),此时可以通过设置几个判断条件,在进入最后的多重循环之前就进行过滤,比如最小3个数的和,已经大于target,或最大3个数的和,小与target。
不过,这样的思路严重缺乏可扩展性,在4数和时就能体会到,要区分的情况有点多,容易想不清楚...
这个技巧有点意思,我在3数和时应用过,Python有点效果,C++没看到效果,C还没有实现,要自己写的代码太多。
思路是这样的:面对一个不带重复数据的已经排好序的序列,找出2个数,和为target,此时通过两次二分查找,可以定位一个这样的小区间,这个区间内一定有一个数满足条件,而另一个数是否存在,通过Hashtable定位。(前面的计算步骤,已经得到了Hashtable)
在面对k数和的时候,应用前面任何一个算法,时间复杂度都会越来越高。而且如果当k作为一个参数的时候,前面的算法都无法应用。即k数和的问题变成:输入一组数据,k和target,找出所有不重复的组合,使得组合中k个数的和等于target。
假设k大于2,序列中共有n个数,有个数为a,判断k数和就等于判断a加上k-1个数的和,以及没有a时的k-1个数的k数和。这是递归思路,下面是kSum的递归实现(通过LeetCode 4Sum的测试):
def kSum1(data: list[int], k: int, target: int) -> list[tuple[int]]:
if not data: # data list must be sorted!!
return []
if k > len(data):
return []
mt = target // k
if mt<data[0] or mt>data[-1]:
return []
if k == 1:
if target in data:
return [(target,)]
return []
r1 = [it+(data[0],) for it in kSum1(data[1:],k-1,target-data[0])]
i = 1
while i<len(data) and data[i]==data[i-1]:
i += 1
r2 = [it for it in kSum1(data[i:],k,target)]
return r1 + r2
这个算法功能OK,但时间复杂度是指数级的!
尝试了几个实现,都是MLE(Memory Limit Exceed)。还未找到更好的DP实现?
我觉得这应该算一个回溯技巧,将不确定嵌套深度的循环,转为递归实现。将循环的嵌套层次数,转为递归深度,有点意思...
def kSum2(data: list[int], k: int, target: int) -> list[tuple[int]]:
def __2Sum(data, target):
r = []
nm1 = len(data) - 1
lo = 0
hi = nm1
while lo < hi:
s = data[lo] + data[hi]
if s<target or (lo>0 and data[lo]==data[lo-1]):
lo += 1
continue
if s>target or (hi<nm1 and data[hi]==data[hi+1]):
hi -= 1
continue
r.append((data[lo],data[hi]))
lo += 1
hi -= 1
return r
if not data: # data list must be sorted!!
return []
mt = target // k
if mt<data[0] or mt>data[-1]:
return []
if k == 2:
return __2Sum(data,target)
r = []
for i in range(0,len(data)-k+1):
if i==0 or data[i]!=data[i-1]:
r += [it+(data[i],) for it in kSum2(data[i+1:],k-1,target-data[i])]
return r
递归调用的深度完全由k控制,每一层都只有一个调用递归的循环,k=2是递归的base condition。本质上这个计算过程还是循环,排序+Two Pointer减少了一层循环,因此时间复杂度为\(O(N^{k-1})\)。
def kSum3(data: list[int], k: int, target: int) -> list[tuple[int]]:
def __3Sum(data, target):
rtv = []
size = len(data)
i = 0
while i < size-2:
if i>0 and data[i]==data[i-1]:
i += 1
continue
t = target - data[i]
lo = i + 1
hi = size - 1
while lo < hi:
s = data[lo] + data[hi]
if s<t or (lo>i+1 and data[lo]==data[lo-1]):
lo += 1
continue
if s>t or (hi<size-1 and data[hi]==data[hi+1]):
hi -= 1
continue
rtv.append((data[i],data[lo],data[hi]))
lo += 1
hi -= 1
i += 1
return rtv
assert k >= 3
if not data: # data list must be sorted!!
return []
mt = target // k
if mt<data[0] or mt>data[-1]:
return []
if k == 3:
return __3Sum(data,target)
r = []
for i in range(0,len(data)-k+1):
if i==0 or data[i]!=data[i-1]:
r += [it+(data[i],) for it in kSum3(data[i+1:],k-1,target-data[i])]
return r
def kSum4(data: list[int], k: int, target: int) -> list[tuple[int]]:
if not data: # data list must be sorted!!
return []
mt = target // k
if mt<data[0] or mt>data[-1]:
return []
if k == 1:
if target in data:
return [(target,)]
return []
r = []
for i in range(0,len(data)-k+1):
if i==0 or data[i]!=data[i-1]:
r += [it+(data[i],) for it in kSum4(data[i+1:],k-1,target-data[i])]
return r
将kSum1,kSum2,kSum3和kSum4放在一起对齐测试
测试代码如下,先确保功能正确(以上代码其实都通过了LeetCode的测试),然后跑时间曲线出来:
# function test
d1 = sorted([1,0,-1,0,-2,2])
t1 = 0
d2 = [2,2,2,2,2]
t2 = 8
k = 4
r1 = [sorted(it) for it in kSum1(d1,k,t1)]
r2 = [sorted(it) for it in kSum2(d1,k,t1)]
r3 = [sorted(it) for it in kSum3(d1,k,t1)]
r4 = [sorted(it) for it in kSum4(d1,k,t1)]
assert r1 == r2 == r3 == r4
r1 = [sorted(it) for it in kSum1(d2,k,t2)]
r2 = [sorted(it) for it in kSum2(d2,k,t2)]
r3 = [sorted(it) for it in kSum3(d2,k,t2)]
r4 = [sorted(it) for it in kSum4(d2,k,t2)]
assert r1 == r2 == r3 == r4
k = 5
for i in range(50,120):
data = [j for j in range(i)]
target = data[i//2]
r1 = [sorted(it) for it in kSum1(data,k,target)]
r2 = [sorted(it) for it in kSum2(data,k,target)]
r3 = [sorted(it) for it in kSum3(data,k,target)]
r4 = [sorted(it) for it in kSum4(data,k,target)]
assert r1 == r2 == r3 == r4
print('ok')
# time test
from timeit import timeit
import time
t1 = []
t2 = []
t3 = []
t4 = []
k = 5
loop_range = range(120,540)
for i in loop_range:
print(i, time.ctime())
data = [j for j in range(i)]
target = data[i//2]
rnum = 3
t1.append(timeit('kSum1(data,k,target)',
number=rnum,
timer=time.process_time,
globals=globals())/rnum)
t2.append(timeit('kSum2(data,k,target)',
number=rnum,
timer=time.process_time,
globals=globals())/rnum)
t3.append(timeit('kSum3(data,k,target)',
number=rnum,
timer=time.process_time,
globals=globals())/rnum)
t4.append(timeit('kSum4(data,k,target)',
number=rnum,
timer=time.process_time,
globals=globals())/rnum)
import time
print(time.ctime())
import matplotlib.pyplot as plt
fig,ax = plt.subplots()
ax.set_title('K = %d' % k)
ax.plot(loop_range,t1,linewidth=0.5,label='kSum1')
ax.plot(loop_range,t2,linewidth=0.5,label='kSum2')
ax.plot(loop_range,t3,linewidth=0.5,label='kSum3')
ax.plot(loop_range,t4,linewidth=0.5,label='kSum4')
ax.legend()
plt.show()
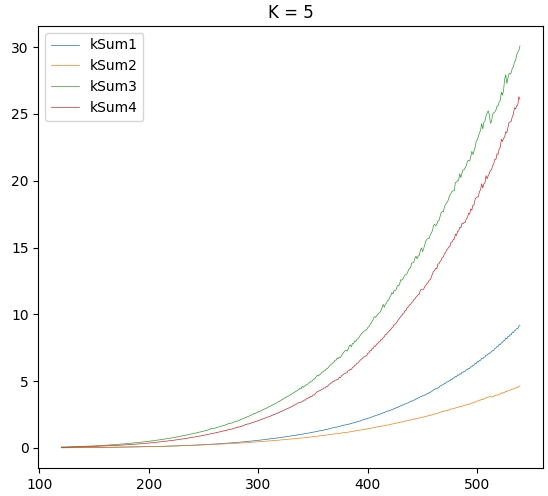
输出曲线:

kSum4的时间复杂度应该是\(O(N^k)\),当k=1时,contain操作也是线性的。但为什么kSum3是最慢的呢?
请参考LeetCode第18题,四数和。
本文链接:https://cs.pynote.net/ag/202310122/
-- EOF --
-- MORE --