二叉树（Binary Tree）

Last Updated: 2024-03-03 06:59:11 Sunday

-- TOC --

二叉树（Binary Tree）
完美二叉树（Perfect Binary Tree）
满二叉树（Full Binary Tree）
完全二叉树（Complete Binary Tree）
二叉树的高度与叶子节点的数量
满二叉树Internal和External节点数量差1

应用开发一般不会直接撸二叉树，Binary Tree，各种库和底层接口已经把它封装好了，但这个东西却是很多系统性能的关键，必须要深刻理解。Heap结构基于二叉树，但实现相对比较简单，很多时候需要我们自己直接手搓Heap实现。

二叉树（Binary Tree）

下面是关于二叉树相关的一些术语。（这些术语也可以用于其它类型的树结构，因为都是一样的概念）

定义：Binary Tree或者Empty，或者是一个Node，这个Node的左右两边包含Value和Reference，Reference的指向也是一颗Binary Tree，即子树Subtree。简单说，二叉树的每个节点除了Value之外，还有两个指针（不能多，也不能少，二叉），这两个指针指向结构一样的节点，或指向空。

Root Node is the top node，树根，根节点
Parent Node，父节点
Child Node，子结点
Leaf Node, which is node with no children，叶子节点
Internal Node, which is node with at least one children，中间节点
External Node，就是Leaf Node，当在讨论决策树模型时，常常使用internal和external这两个词
Edge, lines between any two node，边，两个节点之间的逻辑连接
Level, 层数
Depth of node, the number of node to the root，深度，与层次是同一概念
Height of node, the max number of node to a leaf node，高度，到达Leaf的最长路径，root的height值最高，Height of Tree, is the height of root node。计算高度（Node Height）时，要么数Node，要么数Edge，可根据场景需要看那种方便，最小高度值要么为1，要么为0。不过，数Edge，最小为0是更常见的选择。

For any node n, the depth of n is the length of the unique path from the root to n. Thus, the root is at depth 0. The height of n is the length of the longest path from n to a leaf. Thus all leaves are at height 0. The height of a tree is equal to the height of the root.

B-Tree不是Binary Tree，它是Balanced Tree，虽然最初的B-Tree论文并没有说明B是什么意思...

遍历术语：

preorder traversal，前序遍历
inorder traversal, 中序遍历
postorder traversal，后续遍历
level-order traversal，按depth遍历

前中后均指当前节点相对子节点的顺序。

不管哪种顺序，每个节点都访问并处理一次，时间复杂度为$O(N)$。简单的递归实现，由于二叉树的性质，树的depth，即root depth的期望值远远小于节点数N，因此递归实现不太容易出现过多使用栈空间或超过最大递归深度的问题。其实，在构建树的时候，有很多方法能够保证其平衡性，比如AVLTree，这使得可以放心使用递归遍历算法。

如果不是二叉树，而是更多叉的树形结构，inorder traversal就不太好定义了！

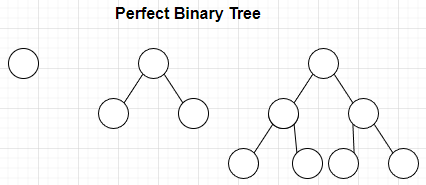
完美二叉树（Perfect Binary Tree）

定义：All internal nodes have 2 children, and all leaves have the same depth. 所有中间节点都有2个子结点，所有叶子节点的深度相同。

perfect_binary_tree

Perfect Binary Tree总是完美的三角形！它是完美的。

满二叉树（Full Binary Tree）

定义：Every node has 0 or 2 children. 每个节点都有0个或2个子结点。

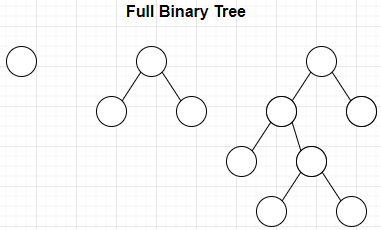
full_binary_tree

Perfect Binary Tree is Full Binary Tree, but not vice versa. 完美二叉树是满二叉树，但反过来不成立。如果只有一个child，就不满了。

满二叉树，就是一颗决策树！

完全二叉树（Complete Binary Tree）

定义：Every level is completely filled maybe except the bottom. Nodes in the bottom level are packed towards the left side. 除了最后一层，其它层的节点是满的，而且最后一层的节点全部靠向左侧。

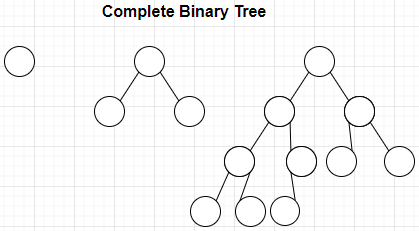
complete_binary_tree

Perfect Binary Tree is Complete Binary Tree, but not vice versa. 完美二叉树是完全二叉树，但反过来不成立。Full Binary Tree may not be Complete Binary Tree. 满二叉树不一定是完全二叉树。

完全二叉树有非常重要的特性：

完全二叉树可以用一个array来实现简单高效的存储。
有了array的index（>=0），就可以直接计算出此index对应node的parent和children的index：
- root节点的index=0
- parent(idx) = (idx-1) // 2，idx>0
- left(idx) = idx*2 + 1
- right(idx) = idx*2+2 or left+1
有child的节点数：len(array) // 2
判断最后一个有child的internal节点是否有右child节点，len(array) & 1，奇数就有右child，此时它还是一颗full binary tree，偶数则没有右child。

链表结构的痛，在于indexing为$O(N)$，如果能将链表转为array（要根据情况具体分析是否值得），可以解决此问题。完全二叉树，它的定义是链表结构，但存储直接就是array！Nice...

二叉树的高度与叶子节点的数量

如果$k$表示某颗二叉树的最大高度，L表示叶子节点数，那么：

$$2^k \ge L$$

$2^k$是高度为k的二叉树可能拥有的最大叶子节点数。

可用Induction证明。

满二叉树Internal和External节点数量差1

就是中间节点和叶子节点的数量差1的意思。

本文链接：https://cs.pynote.net/ag/tree/202306271/

-- EOF --

-- MORE --