Last Updated: 2024-03-01 12:21:10 Friday
-- TOC --
这里所说的堆(Heap)是一种数据结构,与进程虚拟空间中的堆(malloc申请内存的空间)是完全不同的概念,注意区别!
堆(Heap)在逻辑上是一颗完全二叉树(Complete Binary Tree),其父节点和子节点之间,需要满足约定的大小关系。有两种类型的Heap,如下:
maxheap,in any given subtree,the max value must be found in its root,大根堆,任一个节点的值都大于等于两个子节点的值(如果子节点不存在,条件自然满足)。minheap,in any given subtree,the min value must be found in its root,小根堆,任一个节点的值都小于等于两个子节点的值(如果子节点不存在,条件自然满足)。因此,大根堆(maxheap)的root是整个堆中的max节点。小根堆(minheap)的root是整个堆中的min节点!Heap结构巧妙的通过元素间不完全的排序,快速达到这一状态。
对Heap数据结构,有如下几个基本操作:
以上任何操作执行之后,都必须保证Heap结构的特性不变(invariant):
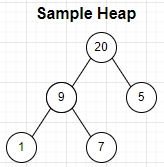
下图是一颗简单的maxheap示例:

Heap结构的存储是一个array,但此array并非完全有序。Heap结构并非要求所有元素有序,仅仅是要求parent与children的关系。如上图,5比7小,但5与7不存在父子关系。
所谓堆排序算法(Heapsort),就是先将待排序的array数据,原地转变成一个heap结构,然后将root元素与heap最后一个元素交换,缩小heap size并将新的root元素trickle down,重复这个动作直到heap size为0。最后得到array就是排好序的了。
Heapsort对空间没有需求,原地排序(in-place),而且不需要递归。
排序算法学习资料:内部排序算法总结
优先级队列(Priority Queue)是堆(Heap)的另一个名称。(有些地方还能看到heap queue的说法)
优先级Queue与普通Queue比较,不一样的地方在于,每次pop(dequeue)出来的总是具有最大(或最小)优先级的元素。其实,实现Priority Queue的方式很多,但性能最好的,就是基于Heap的实现。基于比较的排序算法的理论最快时间复杂度需要\(\Theta(N\cdot\log{N})\),而Heap这种结构,它不追求完全有序,因此它可以在add和pop元素的时候,做到\(\Theta(\log{N})\)。
将Heap应用到Priority Queue时,接口肯定会与应用于Sorting时有所不同。比如可能是直接交换root位置为一个新的元素,或者直接调整某个位置元素的Priority,或者交换一个非root位置为一个新的元素(删除某个元素,用一个新的元素替换,Heap size不变)等等。
BSTree和Heap都可以用来sorting,但是他俩更重要的任务都是干别的事情!
有趣的比较:
FIFO,fair enough!,很公平。unfair!,不公平。LIFO,后进先出,.....从实现的角度看,Queue和Stack,都可以根据情况,采用linked-list方式实现。而Heap只能采用array实现!下面是一个较通用的Heap参考实现和测试,不是性能最好的,如果保持默认的K,它就是个maxheap:
class Heap:
def __init__(self, key=lambda x:x):
self.data = []
self.K = key
@staticmethod
def _parent(idx):
assert idx > 0
return (idx-1) // 2 # same as >>1, not int()
@staticmethod
def _left(idx):
return idx*2 + 1
@staticmethod
def _right(idx):
return idx*2 + 2
def heapify(self, data):
self.data = data
for i in reversed(range(len(data)//2)):
self._trickle_down(i)
def _trickle_down(self, idx=0):
""" trickle down start at idx """
while idx < len(self.data):
left, right = Heap._left(idx), Heap._right(idx)
tidx = idx
if left<len(self.data) and self.K(self.data[tidx])<self.K(self.data[left]):
tidx = left
if right<len(self.data) and self.K(self.data[tidx])<self.K(self.data[right]):
tidx = right
if tidx == idx:
return
self.data[idx], self.data[tidx] = self.data[tidx], self.data[idx]
idx = tidx
def add(self, x):
""" bubble up """
idx = len(self.data)
self.data.append(x)
while idx > 0:
parent = Heap._parent(idx)
if self.K(self.data[idx]) > self.K(self.data[parent]):
self.data[idx], self.data[parent] = self.data[parent], self.data[idx]
idx = parent
continue
return
def peek(self):
ret = None
if self.data:
ret = self.data[0]
return ret
def pop(self):
ret = None
if self.data:
ret = self.data[0]
self.data[0] = self.data[-1]
del self.data[-1]
self._trickle_down()
return ret
def __bool__(self):
return len(self.data) > 0
def __len__(self):
return len(self.data)
def __repr__(self):
return repr(self.data)
import random
h = Heap()
a = [i for i in range(16)]
random.shuffle(a)
for i in a:
h.add(i)
print(h)
for i in range(len(a)+1):
print(h.peek())
assert h.peek() == h.pop()
h = Heap(lambda x:-x)
a = [i for i in range(16)]
random.shuffle(a)
for i in a:
h.add(i)
print(h)
for i in range(len(a)+1):
print(h.peek())
assert h.peek() == h.pop()
按字符串长度排序的Heapsort
h = Heap(lambda x:len(x))
a = [str(i)*i for i in range(9)]
random.shuffle(a)
for i in a:
h.add(i)
b = [h.pop() for _ in range(len(h))]
print(b)
heapify接口
给上面的实现,增加了一个heapify接口,如上!将一个任意的list,直接原地转换成heap结构。下面是测试代码,check_heap是个通用的heap结构checker!
def heap_check(data, K=lambda x:x):
if (size:=len(data)) == 0:
return True
idx = (size//2) - 1
i2 = idx * 2
if size & 1:
t = data[i2+2] if K(data[i2+1])<K(data[i2+2]) else data[i2+1]
if K(data[idx]) < K(t):
return False
else:
if K(data[idx]) < K(data[i2+1]):
return False
for i in range(idx-1,-1,-1):
i2 = i * 2
t = data[i2+2] if K(data[i2+1])<K(data[i2+2]) else data[i2+1]
if K(data[i]) < K(t):
return False
return True
import random
for n in range(2000):
a = [i for i in range(n)]
random.shuffle(a)
h = Heap()
h.heapify(a)
assert len(h) == n
assert heap_check(h.data)
K = lambda x: -x
for n in range(2000):
a = [i for i in range(n)]
random.shuffle(a)
h = Heap(K)
h.heapify(a)
assert len(h) == n
assert heap_check(h.data, K)
原地构建Heap结构,速度是线性的,\(\Theta(N)\)。
上文的heapify接口,就当做伪代码来用吧:
def heapify(self, data):
self.data = data
for i in reversed(range(len(data)//2)):
self._trickle_down(i)
这段代码的逻辑,就是从最后一个有Leaf的节点开始,从后往前,一个个执行trickle down,直到root节点。由于heap逻辑上是一颗完全二叉树,因此,最末端的最后一个有Leaf的节点的index为\(\left\lfloor\frac{\text{heap size}}{2}\right\rfloor\)(index从0开始)。
下面证明这段代码的时间复杂度是Linear级别:
当worst case时,我们对一颗perfect binary tree进行heapify操作,因为此时需要的操作数最多,同时perfect binary tree自然就是一颗complete binary tree。设这颗树的节点数为n,高度为h,有\(\log{n}=h\)。
算法从倒数第2层,即h-1层开始计算,每一次计算都会将subtree的root节点调整到位,为满足worst case的假设,我们可以认为每一次对subtree的调整,都会执行到这颗subtree的leaf层,即最底层。此时,我们一共要进行的操作的总次数为:
\(\sum\limits_{i=1}^h i\cdot 2^{h-i}=\sum\limits_{i=1}^h \cfrac{i\cdot 2^h}{2^i}\le \sum\limits_{i=1}^h \cfrac{i\cdot n}{2^i}\le 2n=\Theta(n)\)
(计算过程:把这个式子展开,可以得到h个等比数列,每个等比数列又都依次小于一个从n开始,比例为1/2的等比数量的各个项,加在一起就是小于2n)
QED
设一个有n个节点的heap,现在要把root节点做trickle down操作,计算时间复杂度。
由于heap是一个complete binary tree,有可能出现left subtree的节点数大于right subtree的情况,worst case的情况为,在left subtree的节点数比right subtree多时,trickle down依然一路执行到left subtree层数最多的leaf位置。
如果right subtree的高度为h,其节点数为\(a=2^{h+1}-1\),此时left subtree的高度为h+1,最大节点数为\(b=2^{h+2}-1=2a+1\),总节点数为\(3a+2\)。此时,我们可以得出,left subtree可能的最大节点数是总结点数的2/3。设\(T(n)\)为n个节点时,root根节点trickle down的时间,那么:
\(T(n) \le T(2n/3) + \Theta(1)\)
根据Master Theory计算,\(T(n)=\Theta(\log_{3/2}n)\),which is asymptotically a bit slower than \(\Theta(\log_2{n})\)。
heapq模块文档:https://docs.python.org/3/library/heapq.html
这个模块的源码,非常值得学习!其对heap结构的实现,更加高效,关键点是_siftup实现以及注释,具体如下:
# The child indices of heap index pos are already heaps, and we want to make
# a heap at index pos too. We do this by bubbling the smaller child of
# pos up (and so on with that child's children, etc) until hitting a leaf,
# then using _siftdown to move the oddball originally at index pos into place.
#
# We *could* break out of the loop as soon as we find a pos where newitem <=
# both its children, but turns out that's not a good idea, and despite that
# many books write the algorithm that way. During a heap pop, the last array
# element is sifted in, and that tends to be large, so that comparing it
# against values starting from the root usually doesn't pay (= usually doesn't
# get us out of the loop early). See Knuth, Volume 3, where this is
# explained and quantified in an exercise.
#
# Cutting the # of comparisons is important, since these routines have no
# way to extract "the priority" from an array element, so that intelligence
# is likely to be hiding in custom comparison methods, or in array elements
# storing (priority, record) tuples. Comparisons are thus potentially
# expensive.
#
# On random arrays of length 1000, making this change cut the number of
# comparisons made by heapify() a little, and those made by exhaustive
# heappop() a lot, in accord with theory. Here are typical results from 3
# runs (3 just to demonstrate how small the variance is):
#
# Compares needed by heapify Compares needed by 1000 heappops
# -------------------------- --------------------------------
# 1837 cut to 1663 14996 cut to 8680
# 1855 cut to 1659 14966 cut to 8678
# 1847 cut to 1660 15024 cut to 8703
#
# Building the heap by using heappush() 1000 times instead required
# 2198, 2148, and 2219 compares: heapify() is more efficient, when
# you can use it.
#
# The total compares needed by list.sort() on the same lists were 8627,
# 8627, and 8632 (this should be compared to the sum of heapify() and
# heappop() compares): list.sort() is (unsurprisingly!) more efficient
# for sorting.
def _siftup(heap, pos):
endpos = len(heap)
startpos = pos
newitem = heap[pos]
# Bubble up the smaller child until hitting a leaf.
childpos = 2*pos + 1 # leftmost child position
while childpos < endpos:
# Set childpos to index of smaller child.
rightpos = childpos + 1
if rightpos < endpos and not heap[childpos] < heap[rightpos]:
childpos = rightpos
# Move the smaller child up.
heap[pos] = heap[childpos]
pos = childpos
childpos = 2*pos + 1
# The leaf at pos is empty now. Put newitem there, and bubble it up
# to its final resting place (by sifting its parents down).
heap[pos] = newitem
_siftdown(heap, startpos, pos)
一开始我也有点疑惑,_siftup(就是trickle_down,一个是将大的沉下去,一个是将小的浮上来)的实现看着有点怪异,newitem在整个循环过程中,完全没有参与比较,而是在最后,调用对应的_siftdown。这样的原因,以及带来的性能优势,需要仔细阅读上面的注释,说的很清楚。简单说,这样非教科书般的实现,可以降低比较的次数,提高性能。
我在解LeetCode第23题(合并K个有序单链表)时,应用了heap数据结构,但实现与本文代码稍有不同,更加高效优雅...C和C++版本的heap实现也在此题内,供参考。
本文链接:https://cs.pynote.net/ag/tree/202401201/
-- EOF --
-- MORE --