学习B-Tree结构

Last Updated: 2024-02-25 14:49:57 Sunday

-- TOC --

B-Tree
B+Tree

一般B-Tree的B被解释为Balance，因为B-Tree在任何时候，都是平衡的。不同于各种BSTree（AVLTree或红黑树等），B-Tree的很矮，每个节点内包含的key数量很多。这种结构在数据库的实现中很常见，因为访问硬盘的性能相对于访问内存来说，慢了好几个数量级，假设B-Tree节点无法全部存放在内存中，矮胖型的B-Tree结构，可以显著减少访问硬盘的次数。

数据库都是直接IO访问硬盘。

B-Tree将所有二叉搜索树一般化了...

B-Tree

B-Tree的特点：

B-Tree有一个minimum degree概念（有人翻译为阶），用$t$表示，$t\ge 2$。
除了root节点之外，其它所有节点，含有的key的数量为$[t-1,2t-1]$。（key数量的上限是个奇数，很妙，因为插入时，算法总是先split，再插入值，避免走回头路）
当节点key的数量为最大时，我们称这个节点full。
root节点例外，比如在刚开始创建B-Tree结构的时候，一个个key被添加到树中，key的数量一定是从0开始，直到root节点key的数量达到$2t$，树结构开始分裂。（先分裂，再插入叶子节点）
在实现时，root节点常驻内存。
节点中key按照从小到大的顺序排序。
设$n$为节点中key的数量，如果此节点是internal节点，那么它刚好就有$n+1$个child。
internal节点child的数量范围$[t,2t]$。
B-Tree所有Leaf节点都在同一高度，即树的高度$h$。（B-Tree结构无论怎么变形，这个特性都能够保证，因此B被认为是Balanced意思）
由于child数量众多，在实现时，有时会在节点结构中，设置有一个字段，用来表示此节点是否为Leaf。Leaf节点没有child，即所有child指针都为NULL。
增加key总是发生在Leaf节点，internal节点都是分裂出来的。

B-Tree的degree最小为2，此时每个internal节点有2,3或4个child，这种树有个名字，叫做2-3-4 tree，有的文献用2-4 tree（注意与2-3 tree进行区别，按B-Tree的定义，2-3 tree不是B-Tree）。最初的红黑树，就是以2-3-4 tree的面貌出现的。红黑树与2-3-4 tree可以相互转化。

B-Tree的高度：

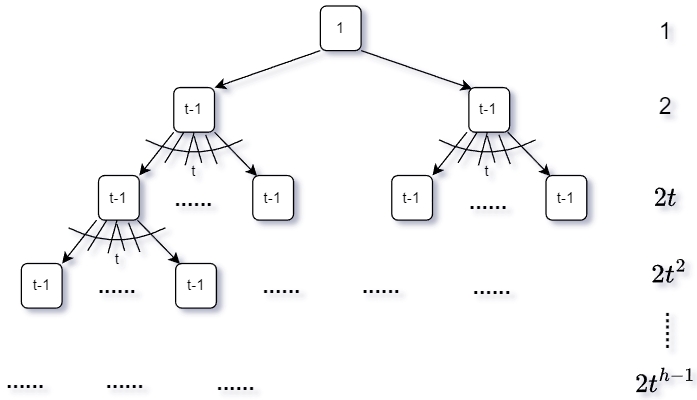
假设key数量为$n$，degree为$t$，高度为$h$，能够画出最高的tallest B-Tree如下：

$$\begin{aligned} 1+2(t^h-1)& \le n \\ t^h & \le \cfrac{n+1}{2} \\ h & \le \log_t\cfrac{n+1}{2} \end{aligned}$$

B-Tree是绝对平衡的，所有Leaf都在同一个Height水平上。
只有root拥有的key的数量，可以小于$t-1$。

同理，就不画图了，最矮的shortest B-Tree，每个节点都有2t-1个key，设高度为h，key的数量为n，

$$h \ge \log_{2t}{\cfrac{n}{(2t-1)2t}}$$

因此，B-Tree的高度就在这两个数之间。

B+Tree

B+Tree是B-Tree的一种变体。

本文链接：https://cs.pynote.net/ag/tree/202402171/

-- EOF --

-- MORE --