Last Updated: 2024-04-27 03:25:43 Saturday
-- TOC --
算法分析是在数学层面证明算法的正确性,同时分析算法的资源需求(时间,空间,带宽或能源消耗,主要是时间复杂度分析),进而能够比较不同算法的性能差异(Order of Growth)。算法分析不是算法实现,用伪代码(pseudocode),是一个纯数学的证明和分析过程。
算法分析最常见(默认)的是Worst Case Analysis,但有时也要根据情况,做Avearge/Expected Case Analysis,少有分析Best Case的情况。当需要考虑概率的时候,有人用Expected这个词,不过《CLRS》书采用Average这个词,而在随机算法时采用Expected:
In general, we discuss the average-case running time when the probability distribution is over the inputs to the algorithm, and we discuss the expected running time when the algorithm itself makes random choices.
手里只有锤子的人,看任何问题都是钉子!算法分析所需要的技能,可能并不是程序员所熟悉的各种编程语言,即锤子。算法分析需要数学,在理论层面做工作。除了锤子,我们还需要利剑和大刀!我们不能只有一个思维模型,我们需要同时具备多种思维模型,并要练就能按需切换和应用的本领。不想当科学家的程序员不是好的投资人!
Computing Model是算法执行环境的抽象,确定Computing Model是算法分析的第1步。
最常用的Computing Model叫做RAM,这个RAM不是指随机访问存储,而是指Random Access Machine计算模型,这是最常用的模型。(或者叫做 uniform cost RAM model)
还有Parallel或Quantum Computing等其他Model...
RAM模型简单好用直接,它将具体计算机体系架构中影响性能的复杂因素统统简化或省略,基本上只考虑CPU提供基本操作,算术逻辑运算,内存读写,控制,并且所有基本操作的cost都认为相同,即每一个操作的cost都是一个基本时间单位(详细分析过程中会带上一个常数系数)。这样,在抽象层面分析算法性能时,只需要计算算法运行过程这些基本操作的数量。像CPU中的cache,虚拟内存等等这些体系架构的东西,完全就忽略不考虑了。RAM模型视角的内存无限大,读写性能一样,用index读写array性能一样,乘法与加法cost相同,都是一个基本时间单元。
但,不要滥用RAM模型:
Strictly speaking, we should precisely define the instructions of the RAM model and their costs. To do so, however, would be tedious and yield little insight into algorithm design and analysis. Yet we must be careful
not to abuse the RAM model. For example, what if a RAM had an instruction that sorts? Then you could sort in just one step. Such a RAM would be unrealistic, since such instructions do not appear in real computers.Our guide, therefore, is how real computers are designed. The RAM model contains instructions commonly found in real computers:arithmetic(such as add, subtract, multiply, divide, remainder, floor, ceiling),data movement(load, store, copy), andcontrol(conditional and unconditional branch, subroutine call and return).
虽然RAM模型很简单,但在其中分析算法复杂度时,有时确很有挑战,需要不少数学知识:
Although it is often straightforward to analyze an algorithm in the RAM model, sometimes it can be quite a challenge. You might need to employ mathematical tools such as
combinatorics,probability theory,algebraicdexterity, and the ability to identify the most significant terms in a formula. Because an algorithm might behave differently for each possible input, we need a means for summarizing that behavior in simple, easily understood formulas.
Lower order terms and constants and also coefficients are all abandoned, only the dominated term is kept!
That is, we are concerned with how the running time of an algorithm increases with the size of the input in the limit, as the size of the input increases without bound. Usually, an algorithm that is asymptotically more efficient is the best choice for all but very small inputs.
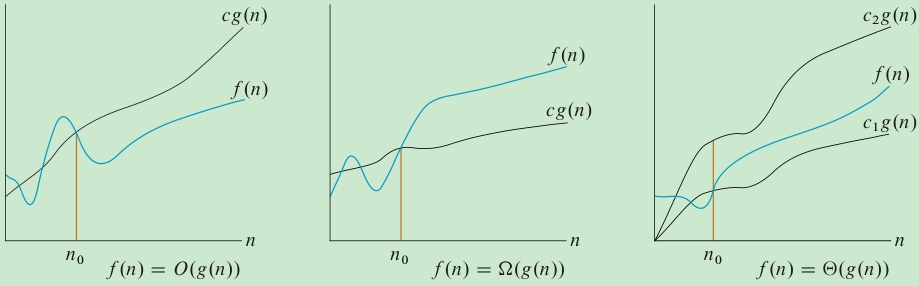
\(O\)-notation
O-notation describes an asymptotic
Upper Bound, also calledBig-Ohnotation. For a given function g(n), we denote by O(g(n)) (pronouncedbig-oh of g of nor sometimes justoh of g of n) the set of functions:
\(O(g(n))=\{f(n): \exist c>0, \exist n_0>0, \forall n\ge n_0, 0 \le f(n) \le cg(n)\}\)
这个正式的定义,说明Big-Oh是一个集合(下同),但习惯上,我们不使用\(f(n)\in O(g(n))\),而是用等号,\(f(n)=O(g(n))\)。如果\(f(n)=O(n^2)\),那么\(f(n)=O(n^3)=O(n^4)\)也都是成立的,但我们要尽量使用最小的order of grow来表达。Big-Oh表达的是at most的意思,它是我们最常用的表达算法复杂度的概念。
当这些Notations单独出现在等号的某一边时,表达\(\in\)的意思。当它们混合出现在等式中时,表达一个具有此asymtotic性质的任意匿名函数。
\(o\)-notation
The asymptotic upper bound provided by O-notation may or may not be asymptotically tight.
\(o(g(n))=\{f(n): \forall c>0, \exist n_0>0, \forall n\ge n_0, 0 \le f(n) \lt cg(n)\}\)
\(\lim\limits_{n\rightarrow \infty}\cfrac{f(n)}{g(n)}=0\),用这个极限做判断可能比用定义更容易,定义中有一个大于0的任意常数,不太好处理。
\(f(n)\) is asymptotically smaller than \(g(n)\) if \(f(n)=o(g(n))\)
\(\Omega\)-notation
Asymptotic Lower Bound.
\(\Omega(g(n))=\{f(n): \exist c>0, \exist n_0>0, \forall n\ge n_0, 0 \le cg(n) \le f(n)\}\)
Big-Omega表达的是at least的意思,证明可能会有点tricky,找出一个input case,证明running time,算法的Lower Bound就一定大于等于此。(也有其他证明方式,比如采用decision tree model证明基于比较的searching或sorting算法的lower bound)
By saying that the worst-case running time of an algorithm is \(\Omega(n^2)\), we mean that for every input size n above a certain threshold, there is at least one input of size n for which the algorithm takes at least \(cn^2\) time, for some positive constant \(c\). It does not necessarily mean that the algorithm takes at least \(cn^2\) time for all inputs.
\(\omega\)-notation
\(\omega(g(n))=\{f(n): \forall c>0, \exist n_0>0, \forall n\ge n_0, 0 \le cg(n) \lt f(n)\}\)
\(\lim\limits_{n\rightarrow \infty}\cfrac{f(n)}{g(n)}=\infty\)
\(f(n)\) is asymptotically larger than \(g(n)\) if \(f(n)=\omega(g(n))\)
\(\Theta\)-notation
Asymptotic Tight Bound.
\(\Theta(g(n))=\{f(n): \exist c_0>0, \exist c_1>0, \exist n_0>0, \forall n\ge n_0, 0 \le c_0 g(n) \le f(n) \le c_1 g(n)\}\)
Theorem
For any two functions \(f(n)\) and \(g(n)\), we have \(f(n)=\Theta(g(n))\) if and only if \(f(n)=O(g(n))\) and \(f(n)=\Omega(g(n))\).
这个定理说明,要证明Tight Bound,需要同时有Upper Bound和Lower Bould。

下面这些说法,都是正确的:
worst case running time of insertion sort is \(O(n^2)\),\(\Omega(n^2)\) and hence \(\Theta(n^2)\).best case running time of insertion sort is \(O(n)\),\(\Omega(n)\) and hence \(\Theta(n)\).When you use asymptotic notation to characterize an algorithm’s running time, make sure that the asymptotic notation you use is as precise as possible without overstating which running time it applies to.
但现实中,人们大多只习惯使用Big-Oh,并且默认Worst Case!
Transitivity
\(f(n)=\Theta(g(n))\ and\ g(n)=\Theta(h(n))\ imply\ f(n)=\Theta(h(n))\)
\(f(n)=O(g(n))\ and\ g(n)=O(h(n))\ imply\ f(n)=O(h(n))\)
\(f(n)=\Omega(g(n))\ and\ g(n)=\Omega(h(n))\ imply\ f(n)=\Omega(h(n))\)
\(f(n)=o(g(n))\ and\ g(n)=o(h(n))\ imply\ f(n)=o(h(n))\)
\(f(n)=\omega(g(n))\ and\ g(n)=\omega(h(n))\ imply\ f(n)=\omega(h(n))\)
Reflectivity
\(f(n)=\Theta(f(n))\)
\(f(n)=O(f(n))\)
\(f(n)=\Omega(f(n))\)
Symmetry
\(f(n)=\Theta(g(n))\) if and only if \(g(n)=\Theta(f(n))\)
Transpose Symmetry
\(f(n)=O(g(n))\) if and only if \(g(n)=\Omega(f(n))\)
\(f(n)=o(g(n))\) if and only if \(g(n)=\omega(f(n))\)
影响算法实际性能的因素非常多,某种编程语言的实现,某次具体的执行,都不可重复,也无法比较。因此,在理论上对算法性能的分析时,与任何具体的实现和执行无关。除了RAM模式(或者根据需要选择其它Computing Model),我们通过编写伪代码,首先证明算法的正确性,然后分析性能指标。
\(T(n)\)代表算法执行时间,n为input size,算法性能表达为\(T(n)=f(n)\),即n的函数。对应的,可用\(S(n)\)表达算法的空间需求。
对于某个算法而言,即使相同的input size,也有可能跑出完全不同的性能,即算法性能与input数据的某些内在特性有关,比如input是否sorted,符合某种概率分布等等。这个insight就是相同input size情况下,case的不同。所以,有的时候会看到,不同case情况下,性能的不同。
不同具体问题的input size可能有所不同,比如sorting算法,input size就是待排序元素的数量,而graph相关算法,input size可能就是vertex和edge两个数量。
两个算法Big-Oh相同,只是表达在input size非常大的情况下,两个算法的order of grow一样,并不是意味着两个算法被实现后,执行时间的完全一样。一个算法的具体执行时间,还跟很多具体的实现细节以及运行环境有关系。而如果input size不够大,似乎一切都没有意义了...
有一种统一的衡量Input Size的方法,就是Bit数来表达。
Big-Oh的定义:
Big-Oh Notation: \(O(g(n))\)
Formally, \(f(n)=O(g(n))\) (pronounce \(f(n)\) is big-oh of \(g(n)\), no equal) means that there exists constants \(c,n_0\),such that \(0 \le f(n) \le c\cdot g(n)\) for all \(n \ge n_0\).
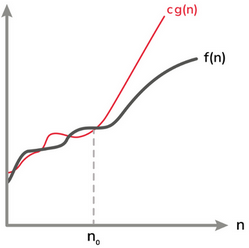
The Big-Oh notation means the rate of growth of running time or needed space. It is the
(tightest asymptotic) Upper Bound of grow rate. In the Big-Oh notation, lower-order term can generally be ignored, and constants can be thrown away. Considerably less precision is required. Big-Oh indicates the(asymptotic) worst-caseon large input size, which wouldnever underestimate!Technically, \(f=O(g)\) does not imply a tight bound. e.g., \(n=O(n^2)\) is true, but \(n^2\) grows much faster than \(n\), but we will generally try to find the tightest bounding of function \(g\).
\(f(n)\)是算法运行时间的估算,也常常用\(T(n)\)来表示。
我们默认认为Big-Oh表达的是asymptotic worse case upper tight bound。CS401的Lab,始终在强调画出upper bound和low bound,这是因为算法的运行时间随input size增加的增长率,与Big-Oh表达式的增长率处于统一级别,通过控制Big-Oh表达式的常数系数,就可以让算法实际运行时间处于三条曲线的中间。Big-Oh表达的是growth rate,与具体的运行时间无关,也因此,在技术上,Big-Oh表达式中去掉了低阶的项和常数系数。
Big-Oh表达式可以存在多个变量,如下:
def nested_loop(n,m):
for _ in range(n):
for _ in range(m):
pass
这个接口的runtime复杂度为 \(O(n\times m)\)
常见的复杂度及其名称如下:
| Complex | Name |
|---|---|
| \(O(1)\) | Constant |
| \(O(\log{n})\) | Logarithmic |
| \(O(n)\) | Linear |
| \(O(n\cdot\log{n})\) | Log Linear |
| \(O(n^2)\) | Quadratic |
| \(O(n^3)\) | Cubic |
| \(O(n^c)\) | Generalized Polynomial |
如果算法是下面这些crazy bad级别的runtime复杂度,算法就算写出来,也基本上是没有实用价值的。input稍微一增大,计算时间就会变得不可接受。(量子计算机呢?)
| Complex | Name |
|---|---|
| \(O(2^n)\) | Exponential |
| \(O(n!)\) | Factorial |
| \(O(n^n)\) |
在表达\(O(\log{n})\)时,不用写出底数是什么,这不重要。不管什么底数,都可以通过换底公式变化,最后也就是多出来一个常数项而已。
\(O(g(n))\),n所表达的magnitude,可以是quantity,也可以是value。比如,计算n的sqrt,n值越大,计算迭代次数就越多。
本文链接:https://cs.pynote.net/ag/202305261/
-- EOF --
-- MORE --