Last Updated: 2024-02-25 14:49:57 Sunday
-- TOC --
BSTree表示二叉搜索树(Binary Search Tree),而AVLTree是最早出现的高度(Height)平衡的BSTree。前置学习内容:二叉树
概念总结:
BSTree:Binary Search Tree,二叉查找树,弥补Binary Search算法无法胜任linked存储结构的遗憾。AVLTree:height-balanced BSTree,AVL是发明人的名字,解决原始BSTree形态可能特别扭曲的问题,确保各种操作的\(O(\log{N})\)复杂度。BSTree定义:每个Parent节点,都大于它的Left Subtree中所有节点,小于它的Right Subtree的所有节点。
BSTree和Heap的区别:
BSTree这个名称中有个Search,说明这个数据结构在Search方面有优势。在BSTree结构中查找某个元素,Worst Case的时间复杂度是\(O(N)\),当添加到BSTree结构中的数据,本就是有序的时候,此时的得到的BSTree,跟一个Linked List没啥区别。
以下是一个BSTree的Python版实现和测试:
class BSTree():
class Node():
def __init__(self, v:int, left=None, right=None):
self.val = v
self.count = 1 # for same value
self.left = left
self.right = right
def __init__(self):
self.size = 0
self.root = None
def add(self, v):
def __add(n, v) -> BSTree.Node:
if not n:
return BSTree.Node(v,None,None)
if v < n.val:
n.left = __add(n.left, v)
elif v == n.val:
n.count += 1
else:
n.right = __add(n.right, v)
return n
self.root = __add(self.root, v)
self.size += 1
def __iter__(self):
""" inorder traversal """
def __iter(n):
if n:
yield from __iter(n.left)
for i in range(n.count):
yield n.val
yield from __iter(n.right)
yield from __iter(self.root)
def __contains__(self, v):
def __contains(n, v) -> bool:
if not n:
return False
if v < n.val:
return __contains(n.left, v)
if v == n.val:
return True
if v > n.val:
return __contains(n.right, v)
return __contains(self.root, v)
def remove(self, v):
def __remove(n, v) -> BSTree.Node|None:
if v < n.val:
n.left = __remove(n.left, v)
return n
if v > n.val:
n.right = __remove(n.right, v)
return n
# v == n.val
if n.count > 1:
n.count -= 1
return n
# n.count == 1
if not n.left and not n.right:
return None
if n.left and not n.right:
return n.left
if not n.left and n.right:
return n.right
# if n.left and n.right,
# replace n by the biggest node from left side.
t = n.left
if not t.right:
n.left = t.left
else:
while t.right:
p = t
t = t.right
p.right = t.left
n.val = t.val
n.count = t.count
return n
if v not in self:
raise ValueError
self.root = __remove(self.root, v)
self.size -= 1
def __len__(self):
return self.size
测试代码:
import random
bst = BSTree()
a = [i for i in range(16)]
random.shuffle(a)
for i in a:
bst.add(i)
bst.remove(4)
bst.remove(5)
bst.remove(10)
bst.remove(11)
bst.add(4)
bst.add(5)
bst.add(6) # duplicate 6
bst.add(6) # duplicate 6
print([i for i in bst])
for n in range(1000):
bst = BSTree()
a = [i for i in range(n)]
random.shuffle(a)
for i in a:
bst.add(i)
assert [m for m in bst] == sorted(a)
random.shuffle(a)
for i in a:
assert i in bst
bst.remove(i)
assert i not in bst
assert len(bst) == 0
remove的实现稍微复杂一点点,找到需要remove的节点后,需要用它左边最大的节点(前驱节点,或者右边最小的节点,后继节点)来替换它。而所谓的二叉树排序算法,就是利用BSTree结构,先add所有元素,然后中序遍历,得到的数据就是排好序的。上述代码中,那个__iter实现的中序遍历太酷了!
排序算法笔记中,有一个C语言版的BSTree实现。
二叉树排序
bst = BSTree()
a = [i for i in range(16)]
random.shuffle(a)
for i in a:
bst.add(i)
b = [i for i in bst]
print(b)
print([i for i in reversed(b)])
判断节点的高度
def height(n):
if not n:
return 0
return 1 + max(height(n.left),height(n.right))
bst = BSTree()
assert height(bst.root) == 0
for i in range(10):
bst.add(i)
assert height(bst.root) == i+1
计算某节点下面的叶子节点数
def leaf_count(n):
if not n:
return 0
if not n.left and not n.right:
return 1
return leaf_count(n.left) + leaf_count(n.right)
BSTree as a mapping structure!
上述实现,node结构中只有一个value,如果即有key,也有value,就可以实现一组mapping API,背后是某种BSTree的结构。add接口对应__setitem__,需增加__getitem__,因为单单一个__contains__是不够的,remove接口对应__delitem__。没啥根本变化......C++ STL中的set和map容器,就是这个思路,只不过肯定不会使用原始的BSTree,而是各种平衡变体。
BSTree中的最值
前驱节点,后继节点
删除节点的时候,会用到这两个概念其中的一个!
如果待删除的节点同时存在左右child,找到predecessor或successor后(称为X),其实从树形结构上看,真正删除的是X这个点。
原始的BSTree,由于可能存在特别扭曲的(skewed)树形结构,导致其时间复杂度为\(O(N)\),甚至有可能因为Depth太深而导致查找时栈空间过多占用,或超过了系统最大允许的recursion limit。最高效查找性能来自左右两侧相对平衡的树形结构。AVL树是最早被发明的自平衡BSTree。在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度(height)平衡(二叉查找)树,各种操作的性能都是\(O(\log{N})\)。
AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。(还有很多著名的算法,用发明者来命名,比如RSA,KMP,哈夫曼编码等等)
二叉树有两种平衡,
weight balanceorheight balance,前者表示左右两侧的节点数的差在某个阈值内,后者表示左右两侧的高度差在某个阈值内。AVLTree属于后者,阈值为1,即高度差不能超过1。
一颗Height相对平衡的BSTree,depth不需要太深,就足够容纳非常多的元素:
# max number of elements of a balanced bstree with depth 24
>>> 2**24
16777216
AVLTree实现的关键,就是在add和remove的时候,及时进行rebalance操作。而rebalance操作的关键,就是rotation,right add/or left rotation!
新增节点时,共有4种rotation场景:
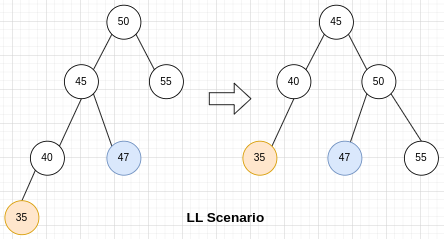
LL

LL场景(Left subtree Left side)就是向右做一次rotation。新增35,只rotate一次,注意47的变化,subtree的height不变,不影响更高层的节点。
RR
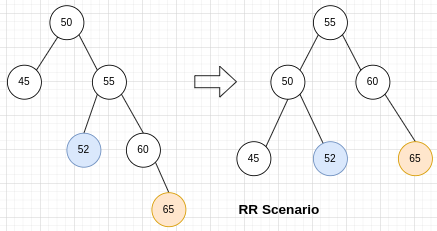
RR场景(Right subtree Right side)就是向左做一次rotation。新增65,只rotate一次,注意52的变化,subtree的height不变,不影响更高层的节点。
LL和RR是
single rotation,左右对称,mirror image symmetry。
LR
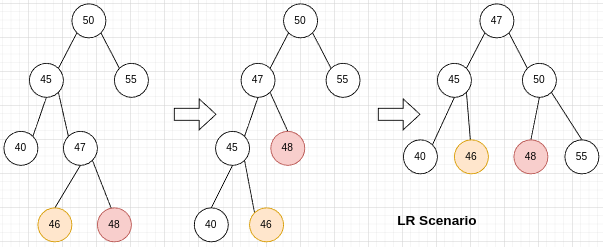
LR场景(Left subtree Right side)要做两次rotation,先向左(node50的left subtree),再向右(node50)。46和48是左右两种情况,处理稍有不同。两次rotation后,subtree的height不变。
RL
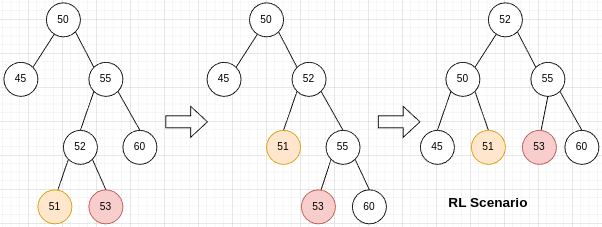
RL场景(Right subtree Left side)要做两次rotation,先向右(node50的right subtree),再向左(node50)。51和53是左右两种情况,处理稍有不同。两次rotation后,subtree的height不变。
LR和RL是
double rotation,左右对称,mirror image symmetry。
删除节点
增加节点后,经过rotation,子树的height保持不变,但这个性质在删除节点时可能无法保持(不是删除所有的元素,都会破坏AVLTree的性质)。子树经过rotation后,height可能会变小,这会对更高层的子树带来影响。因此,删除节点后,要沿着parent往上一个个check节点的balance factor(AVLTree的性质,左右子树的高度差不能大于1)是否得以保持,如果不是,就要对其进行相应的rotation。
Python参考实现
如下是我的AVLTree的Python实现:
class Node():
def __init__(self, v, left=None, right=None):
self.val = v
self.count = 1
self.height = 1 # count node
self.left = left
self.right = right
def rotate_left(self):
n = self.right
self.val, n.val = n.val, self.val
self.count, n.count = n.count, self.count
self.left, self.right, n.left, n.right = \
n, n.right, self.left, n.left
n.height = max(Node.H(n.left),Node.H(n.right)) + 1 # n first
self.height = max(Node.H(self.left),Node.H(self.right)) + 1
def rotate_right(self):
n = self.left
self.val, n.val = n.val, self.val
self.count, n.count = n.count, self.count
self.left, self.right, n.left, n.right = \
n.left, n, n.right, self.right
n.height = max(Node.H(n.left),Node.H(n.right)) + 1
self.height = max(Node.H(self.left),Node.H(self.right)) + 1
@staticmethod
def H(n):
""" return node n's height, if None return 0. """
return n.height if n else 0
def rebalance(self):
if Node.H(self.left) > Node.H(self.right):
if Node.H(self.left.left) >= Node.H(self.left.right):
self.rotate_right() # LL
else:
self.left.rotate_left() # LR
self.rotate_right()
else:
if Node.H(self.right.left) > Node.H(self.right.right):
self.right.rotate_right() # RL
self.rotate_left()
else:
self.rotate_left() # RR
class AVLTree():
def __init__(self):
self.size = 0
self.root = None
def add(self, v):
def __add(n, v):
if not n:
return Node(v,None,None)
if v < n.val:
n.left = __add(n.left, v)
elif v == n.val:
n.count += 1
return n
else:
n.right = __add(n.right, v)
n.height = max(Node.H(n.left),Node.H(n.right)) + 1
if abs(Node.H(n.left)-Node.H(n.right)) >= 2:
n.rebalance()
return n
self.root = __add(self.root, v)
self.size += 1
def __iter__(self):
def __iter(n):
if n:
yield from __iter(n.left)
yield n.val, n.count, n.height
yield from __iter(n.right)
yield from __iter(self.root)
def __contains__(self, v):
def __contains(n, v):
if not n:
return False
if v < n.val:
return __contains(n.left, v)
if v == n.val:
return True
if v > n.val:
return __contains(n.right, v)
return __contains(self.root, v)
def remove(self, v):
def __remove(n, v):
to_fix = [n]
if v < n.val:
n.left = __remove(n.left, v)
elif v > n.val:
n.right = __remove(n.right, v)
else: # n.val == v
if n.count > 1:
n.count -= 1
return n
# n.count == 1
if not n.left and not n.right:
return None
if n.left and not n.right:
return n.left
if not n.left and n.right:
return n.right
# if n.left and n.right
t = n.left
if not t.right:
n.left = t.left
else:
while t.right:
to_fix.append(t)
t = t.right
to_fix[-1].right = t.left
n.val = t.val
n.count = t.count
for t in reversed(to_fix):
t.height = max(Node.H(t.left),Node.H(t.right)) + 1
if abs(Node.H(t.left)-Node.H(t.right)) >= 2:
t.rebalance()
return n
if v not in self:
raise ValueError
self.root = __remove(self.root, v)
self.size -= 1
def __len__(self):
return self.size
下面是测试代码,用到了两个辅助接口:
def height(n):
if not n:
return 0
return max(height(n.left),height(n.right)) + 1
def traverse(n):
if n:
yield from traverse(n.left)
yield n
yield from traverse(n.right)
a = AVLTree()
for i in range(10):
a.add(i)
for v,c,h in a:
print(v,c,h)
for n in traverse(a.root):
print(n.val)
a = AVLTree()
num = [i for i in range(2000)]
for i in num:
a.add(i)
assert i in a
for n in traverse(a.root):
assert height(n) == n.height
assert abs(height(n.left)-height(n.right)) < 2
import random
random.shuffle(num)
for i in num:
a.remove(i)
assert i not in a
for n in traverse(a.root):
assert height(n) == n.height
assert abs(height(n.left)-height(n.right)) < 2
Everything is OK...:),通过了CS401的Lab测试。
通过类似traverse这样的外部接口,可以实现各种顺序的遍历。
__iter__有点难度,需要用到一个stack配合。class BSTree():
class Node():
def __init__(self, v, left=None, right=None, *, parent=None):
self.val = v
self.count = 1
self.left = left
self.right = right
self.parent = parent
def __init__(self):
self.root = None
self.size = 0
def add(self, v):
if not self.root:
# only root has None parent
self.root = BSTree.Node(v, parent=None)
else:
n = self.root
while True:
if v < n.val:
if not n.left:
n.left = BSTree.Node(v, parent=n)
break
n = n.left
continue
if v > n.val:
if not n.right:
n.right = BSTree.Node(v, parent=n)
break
n = n.right
continue
# v == n.val
n.count += 1
break
self.size += 1
def __iter__(self):
if not self.root:
return
stack = []
n = self.root
stack.append(n)
while True:
if n.left:
stack.append(n.left)
n = n.left
continue
n = stack.pop()
while True:
for i in range(n.count):
yield n.val
if n.right:
stack.append(n.right)
n = n.right
break
if len(stack):
n = stack.pop()
else:
return
def __contains__(self, v):
if not self.root:
return False
n = self.root
while True:
if v < n.val:
if not n.left:
return False
n = n.left
continue
if v > n.val:
if not n.right:
return False
n = n.right
continue
# v == n.val
return True
def remove(self, v):
if not self.root:
raise ValueError
else:
n = self.root
while True:
if v < n.val:
if not n.left:
raise ValueError
n = n.left
continue
if v > n.val:
if not n.right:
raise ValueError
n = n.right
continue
# v == n.val
if n.count > 1:
n.count -= 1
break
if not (n.left and n.right):
t = n.left if n.left else n.right if n.right else None
# root
if not n.parent:
self.root = t
if self.root:
self.root.parent = None
break
# not root
if v < n.parent.val:
n.parent.left = t
else:
n.parent.right = t
if t:
t.parent = n.parent
break
# if n.left and n.right,
# replace n by the biggest node from left side.
t = n.left
if not t.right:
n.left = t.left
if t.left:
t.left.parent = n
else:
while t.right:
p = t
t = t.right
p.right = t.left
if p.right:
p.right.parent = p
n.val = t.val
n.count = t.count
break
self.size -= 1
def __len__(self):
return self.size
递归版和循环版BSTree性能比较
根据我个人积累的经验,一般情况都是循环比递归快。
import random
import time
data0 = []
data1 = []
data2 = []
for n in range(2000):
a = [i for i in range(n)]
data0.append(a)
b = a[:]
random.shuffle(b)
data1.append(b)
c = a[:]
random.shuffle(c)
data2.append(c)
tic = time.time()
for i in range(2000):
bst = BSTree_recur() # recursive version
for j in data1[i]:
bst.add(j)
assert [m for m in bst] == data0[i]
for j in data2[i]:
assert j in bst
bst.remove(j)
assert j not in bst
assert len(bst) == 0
print('BST(recur):', time.time() - tic)
tic = time.time()
for i in range(2000):
bst = BSTree() # loop version
for j in data1[i]:
bst.add(j)
assert [m for m in bst] == data0[i]
for j in data2[i]:
assert j in bst
bst.remove(j)
assert j not in bst
assert len(bst) == 0
print('BST(loop):', time.time() - tic)
输出:
BST(recur): 23.155863285064697
BST(loop): 7.092304468154907
本文的代码,足够合成此版本,略!
本文链接:https://cs.pynote.net/ag/tree/202308031/
-- EOF --
-- MORE --