
Last Updated: 2023-09-21 09:14:29 Thursday
-- TOC --
《数学与生活》这本书的作者是日本人,远山启,因此我就直接看中文版的了。读书记笔记的好处,笔记可以起到非常好的refresh memory的效果。这本书很早就有,也有多个翻译的版本,不同版本的中文名也不全相同。
数学是对一切事物的最高层次抽象和表达...
人类的数学知识,是从最最基本的数数开始的。我相信上古时期的人必须要去数数,也是当时的生活所迫,有需求了。
远古时期,数数似乎是件挺困难的事情。历史上出现过许多不同的进制(当时的人还不太能意识到进制这个概念),好多不同的计数方法。文明的消亡在远古时期就是家常便饭,一同消亡的还有文明特有的数数和计数的方式。一般都是有先进数数和计数方式的文明,能够战胜不够先进的甚至还不能数数的文明。所以,最后流传下来的数学知识都是比较先进的,而这些先进的方法,本质上就是最简单的方法。比如用手指的数量来计数而形成的5进制或10进制。
古罗马的计数系统不是基于位置的,而是很像古埃及的计数,与位置无关,只需要加减和求和。古巴比伦的计数系统就是基于位置的系统,但是远没有现在的计数系统那么简洁明了,估计也是技术手段达不到,他们当时只能在泥板上刻,没有纸笔。不清楚是不是古巴比伦的基于位置的计数系统传到了印度,被印度人发扬光大,然后据说是在13世纪初期,又被阿拉伯商人引入欧洲,最后成为一统天下的基于位置的10进制计数系统。
《CSAPP》中有一段描述:The familiar decimal, or base-10, representation has been in use for over 1000 years, having been developed in India, improved by Arab mathematicians in the 12th century, and brought to the West in the 13th century by the Italian mathematician Leonardo Pisano (ca.1170 to ca.1250), better known as
Fibonacci.
因为,这套基于位置的10进制计数系统,足够简单,也非常强大,能够表示任意数字。有了这套最底层计数系统作为工具,之后的数学发展,突飞猛进,进而也让其它科学得以发生和发展。
基于位置(Positional Notation)的进位计数系统,不仅仅可以用于10进制,它可以用于任意进制。比如2进制,计算机能够实现复杂计算,也得益于这套基于位置的2进制计数系统。我们现在把这套最先进的计数系统,在幼儿园时期就教会给了小朋友,他们会认为用这种方式计数,自然而然,天经地义,理所当然。其实,人类是经过了漫长的努力,才彻底解决了数数和计数的问题。
基于位置的计数系统
十进制(含小数部分):
\(x=x_{n-1}10^{n-1}+x_{n-2}10^{n-2}+...+x_010^0+x_{-1}10^{-1}+x_{-2}10^{-2}+...\)
二进制(含小数部分):
\(x=x_{n-1}2^{n-1}+x_{n-2}2^{n-2}+...+x_02^0+x_{-1}2^{-1}+x_{-2}2^{-2}+...\)
二进制整数补码:
\(x=-x_{n-1}2^{n-1}+x_{n-2}2^{n-2}+...+x_02^0\)
罗马数字表示法
LeetCode有两道题,实现整数与罗马数字的相互转换,我们可以从这两道题中,体会基于加减法的古代罗马的计数体系。
离散量,是多少个,比如数一数有多少个苹果,离散数学就是专门研究离散量的数学。连续量,是多少,比如水的多少升。
离散量和连续量可以相互转化。连续量的测量,要靠离散的单位量(有许多不同的单位),而离散的几个土豆,也可以全部捣烂成土豆泥并混在一起成为某种连续的东西。
我在想,比如水,在微观下就是离散的水分子,只是宏观上,我们把它当成连续量来处理。
对连续量的测量,因为有零头存在,就抽象出了小数和分数。在古代,分数的计算是相当复杂繁琐的,因为当时的人们不懂得\(\frac{2}{5}=\frac{1}{5}+\frac{1}{5}\)这样简单的规则。古埃及人甚至发现\(2\div7=\frac{1}{12}+\frac{1}{51}+\frac{1}{68}\),其计算过程更加复杂。从这件事情可以看出,人类思想和技术的发展,一开始并不简单,而发展的过程就是简单化的过程。
笛卡尔想到了用长度来表示连续量,进而创造了坐标系这样的神器,真是天才。连续量很多,用长度来表示,就可以很容易的分割,比较,合并。两个连续量的关系,就可以形成坐标系中的曲线。
分数与小数和整数有一处不一样的地方,同样的一个量的分数,其表现形式可以有无数种,即分子和分母同时乘或除相同的数,并不会改变它所代表的量。因此,我们在比较不同分数的大小时,会通分,即将分母变成一样的,然后比较分子的大小即可。进行分数加减运算的时候,也是要将分母进行通分后才能顺利进行。
乘法最初的含义是加法的扩展,在有分数的时候,乘法的含义被扩展了,乘一个分数,等于乘分子除分母,分数本身自带一个除法。数学相当严禁,也足够灵活自由。从此,乘法不再是增大,乘法也可能变小。
除以一个分数应该如何理解呢?包含分割。(除以整数,我们可以采用水平分割的思想,就是分成多少份)举个包含分割的例子:将一段3米长的铁丝,按1/5米分割,能够分成多少段。这样就能够理解除一个分数,等于除分子再乘分母。从此,除法不再是减少,还可以变大。
分数可以考虑成单位量是余量的多少倍,而小数则是将单位量分成10份,100份(十进制)......后余量占多少份。小数就是用10,100,100......等特殊的数作为分母的分数。今天的十进制小数,是16世纪欧洲发明的。古希腊的欧几里得不懂小数。
有限小数写成分数很容易,分母就是10的幂次数。而把分数写成小数,就要做除法。分数变成小数,不是有限小数,就是无限循环小数,两者避居其一!因此,分数的表达力我觉得是强于小数的!将循环小数转化为分数,就需要一点技巧,有一个方法是用\(\frac{1}{9}\),\(\frac{1}{99}\),\(\frac{1}{999}\) ......作为分母,然后根据具体的循环部分来搞定分子。
无限不循环的小数,无法写成分数,叫做无理数,例如神秘的e!
纯数学世界,都是数字,但是如果是现实世界,量都是有单位的。乘除法会产生新的量,而加减法不会,比如长度乘长度等于面积,面积就是新的量,而长度和面积做加减,没有意义。我觉得就是因为乘除法会产生新的量,因此先乘除后加减!
牛顿观察到的:从自然数的乘法规则中,仅靠推理导不出分数乘分数的规则。数学是高度的抽象,但是最最基本的计算规则,还是来自实践。
0不是正数,也不是负数,0就是0。(0属于自然数)
《沉思录》中有一句话:我了解不理解从0减去4等于0的那些人。
负负得正的规则,跟分数乘法规则一样,不是推导出来的,是无数事实总结出来的。(当这些最基本的计算规则都确定了之后,现实世界的问题就统统要转换成符合这些规则的表达方式)
有理数的域:分数(含无限循环小数)是有理数,加上正负整数,在它们之间无限次的加减乘除,得到的还是有理数。
(我们现在认为理所当然的东西,都经历过漫长的发展,以后未来的人认为理所当然的东西,就由我们在这里苦苦求索)
代数是算术的普遍形式。(机器能有抽象的能力吗?)
交换律:
\(a+b=b+a\),\(ab=ba\)
结合律:
\((a+b)+c=a+(b+c)\),\((ab)c=a(bc)\)
分配率:
\((a+b)c=ac+bc\)
代数学的重要任务之一,就是解方程。而移项是方程变换中最重要的规律。
阿拉伯数学家阿尔.科瓦利兹米(约780-850),把移项叫做al-jabr,因此这个al-jabr就成了现在的algebra,代数学就是所谓的移项学。(代数的历史)
算术是直接计算,方程式因为需要移项,就是反向的计算。
把代数称为灵活的算术,是爱因斯坦的一位当工程师的叔叔说的。
书中对线性代数中的向量和矩阵的计算的描述,让我有一种感觉,矩阵的计算是为了简化计算,浓缩数学表达式,让矩阵计算的表达力变得很强!两个矩阵的加减,可以理解为一组量的加减同时计算,矩阵的乘法,可以看成是在组合计算一些值。在解一组联立方程的时候,矩阵和向量的表达方式,简洁有力!而且还能简化计算过程(这有点像语义表现力很强的python)。拉普拉斯说过一句话:在数学上发明了优越的符号,就意味着成功了一半。
注意一个细节,两个不为0的矩阵相乘,结果可能是0矩阵。
中世纪欧洲,古登堡(1400-1468)制造了最早的活字印刷机,最早印刷的书是《圣经》,然后是欧几里得的《几何原本》。这两本书代表了欧洲文化的两大支柱。
《圣经》是信仰,而《几何原本》则是思维方式。
点(没有大小不可再分),线(没有宽度),角构成了图形的原子。
分析,把复杂的东西分割成简单的单位进行研究,就是分析。这是很重要的一个思维方式。分析之后还要综合。(计算机的层次化思维方式,机制和策略一层层分割,越到底层就越细分,上层都是底层的某种综合)
公理(axiom),比如两点确定一条直线,就像是最最简单的无需言明的常识;而定理(theorem),则需要通过公理和逻辑推演出来。公理+逻辑推演=定理,这也是整个数学的思维方式。(概念是逻辑的起点,概念就像公理一样,定义概念是非常重要的权力)任何需要多人对话的文明,都需要在对话者之间,有共同的基础,这个基础就是公理,就是概念。
从最简单的事实,推导出复杂的难易置信的结果。
逻辑的路径不止一条:直接证明,反证,倒推,归纳。
圆和直线,似乎是最完美最简单的两个图形。由圆和直线,可以组合成各式各样的形状(但不是所有),中世纪哥特式建筑,主要就是圆和直线。画出圆和直线所需要的工具,也是最简单最容易制作的。
哥白尼的日心说,认为天体的轨道是圆;一个世纪后的开普勒才认识到了椭圆。而建筑风格也在朝向椭圆的方向发展。
古希腊的柏拉图推崇只用直线和圆作图,认为只有直线和圆是神圣的,其它形状都是丑陋的。由于柏拉图的影响力,在当时也就限制了其它作图工具的发展和使用。
本章提到了无理数的发现。历史不会简单的重复,每当一个全新的东西被发现或发明,由于不同相关方的利益冲突,总会掀起一些波澜。无理数的发现被称为第一次数学危机,其否定了毕达哥拉斯学派的万物皆是数的思想。
无理数和有理数一样,普遍存在,研究一下连续的数轴就明白了。实数=有理数+无理数。
数学中蕴含着最狂野的思想!

这一章从二次方程的求解开始。
在面对现实问题的时候,代数是慷慨的,二次方程的2个解,往往那个负数解与现实不能对应,是免费送的。在实数域没有解的时候,数学家又开始创造新的数,这就是虚数。数学家不喜欢例外。
实数+实数i = 复数,\(i^2=-1\),复数可以用平面上的点来表示,这个平面也叫高斯平面,但最先想到用平面来表示复数的,是比高斯还早100面左右的测量工程师韦塞尔。
数的绝对值是用\(|x|\)来表示,向量的长度,用\(||v||\)表示,很相似!他们的含义,都是距离O点的距离。所以,数值和(向量)长度是同一个概念。
有了复数之后,所有代数方程都有了解。
复数的加减,以及与实数相乘,规律都与二元向量一致。\(\times\)i,在复数平面上相当于逆时针转动90度。
复数的乘除,与向量的点乘(dot product)是不一样的!复数的乘法可以理解为两个复数的长度相乘,然后再旋转一个角度,其结果很可能还是一个复数。而向量的点乘,结果就是一个数。(Python中可直接进行复数运算)
二次方程的两个复数根,以实数轴为中心线对称,共轭!(是不是有共同的实数部分的复数)
由于乘复数带有旋转的含义,作者用求解正多边形的作图,引入多次方程。
三次方程求解公式比较复杂,而且有一个情况,就是在计算过程中,会出现复数,但是最后的解却都是实数。代数如果没有虚数,看起来是不完整的。

我们可以把解方程看做四则运算的逆运算,逆运算一般都是比较难的。而在进行这个逆运算的过程中,只是用实数是不够的,遇到负数开方就没辙了,因此引入了新的虚数。
代数学的基本定理,在高斯20岁的毕业论文中得到证明。在复数域内,任何方程的根的个数与最高次数相等,即一定有根,根的数量与最高次数相同。
从小到大接触到过很多数字魔术,基本都是一些整数间有趣的关系,这样的事情从古希腊时期就开始了,有一些渐渐成为科学研究的对象。
完全数,数=它所有约数之和,6,28,496,8218.........
又是高斯发明的恒等式:\(a \equiv b \ (mod \ 3)\)
这个恒等式的含义是:a和b做模3的运算,结果恒等。这里面有一个细节一定要理解,模运算的结果一定是0到模数之间,比如mod 3,结果一定是0,1,2之中。(参考python中的模运算)
古时人们用mod这种思想来对事物进行分类。(模运算的结果能否直接被成为余数?反正书中是这么说的。)
已经不记得是什么时候天天在学的东西了:最小公倍数,最大公约数。没有最大的公倍数,最小公约数1无意义。
加法世界的原子是1,乘法世界的原子是素数(prime number),不知是幸运还是不幸,素数也有无限多个。
与素数对应的是合数,合数的素数分解具有唯一性!用这个唯一性定义,还能证明某个数是无理数。
算术和几何是不变的,代数的解方程也是不变的,从函数开始,数学开始动了起来。把代数中的字母看作是变动的数,从笛卡尔开始。
这一章提到了数学家更像画家和诗人,但我却没啥笔记要做,似乎我对函数的熟悉程度远超过前面所有章节。
function与equation是不同的概念,function要满足唯一的输入(定义域domain)得到唯一的输出(值域range)这一特性,而equation则不需要,只要满足相等即可。
函数有很多性质:唯一,奇偶,反,复合......
一段有限长度的线段中有无穷个点,可以无限细分。而极限则是将无穷变成固定值的神奇变换。
运动一旦开始,无穷的现象就必然出现。书中说古希腊的人都想逃避掩盖无穷的问题,包括欧几里得。
步行者追赶乌龟的问题,产生了一个收敛的无穷级数,从这个角度去理解无穷和级数。

当把有限个数相加时,无论如何变换有限个数的顺序,结果都不变。但,无限个数相加时,这条规则就不成立。柯西观察到,只要按照原有的顺序计算,无穷的悖论就不会产生。柯西还注意到,无穷级数的和是可以不存在的!
算术和代数,没有变化和运动;而微积分中提出了变化和运动,极限的计算就成了并列于加减乘除的一种重要的运算。

收敛有速度快慢之分,也有不同的形式。有的从左边,有的从右边,有的来回摆动。
当lim求极限加入到四则运算之后:
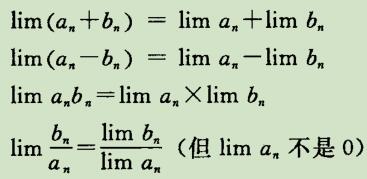
本章从复利开始,引出指数。用指数来表示非常大和非常小的数,是非常方便的。
数学就是一种符号语言。而指数这种符号很精妙,指数部分可以是正数,负数,还可以是分数,甚至无理数,总之,数学家不喜欢例外。(就像编写一个通用的 def function)
有了指数,接着就是对数,然后三角函数也有介绍,这是微积分的函数基础部分。
余弦定理:

当C=90度时,这就是勾股定理。因此余弦定理有更好的普遍性。
正弦定理:
两点确定一套直线,(非同一直线上的)三点确定一个圆!

(以前是怎么学习的,竟然对这两个定理如此陌生)
正弦定理和余弦定理都是三角形角度和边长的关系,而海伦公式就是三角形边长和面积的关系。
海伦公式:

用海伦公式来求三角形的面积,就不需要去求三角形的高了。
这部分最后介绍了欧拉公式,看不懂呀......
牛顿是物理学家。
Line approximation,线性近似,以直代曲,无限逼近,极限是一个固定的值。
在微积分出现之前,人们计算由曲线围成的面积,是很费劲的。
积分的方法,基本思路,就是分段,比如分成n段,每一段就好办了,然后把每一段加起来,然后n-->无穷。
积分的符号,就是拉长了的求和符号,都是S的变体。
这种无限细分(微分)再加总(积分)的思维方式,从阿基米德时代就有了。而之所以说牛顿和莱布尼茨发明了微积分,是因为他们发现微分和积分互为逆运算。
方程不是函数,方程是等式,满足等式条件的变量之间的完整的关系说明,这种关系不一定是函数关系。
微分方程,就是等式中含有微分,即除了有变量,还有变量间的微分关系。
数学讲究的是思维方式,再辅以计算手段......数学符号就是用来表达思维的有力工具,再经过演算,常常得出惊人的结论。数学是朴实的。
本文链接:https://cs.pynote.net/math/202109093/
-- EOF --
-- MORE --