-- TOC --
In mathematics, physics and engineering, the sinc function, denoted by \(sinc(x)\), has two forms, normalized and unnormalized.
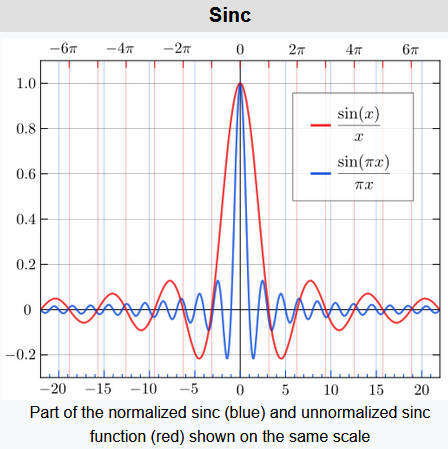
In mathematics, the historical unnormalized sinc function is defined for \(x \neq 0\) by \(sinc(x)=\cfrac{\sin{x}}{x}\)
Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(x).
In digital signal processing and information theory, the normalized sinc function is commonly defined for \(x \neq 0\) by \(sinc(x)=\cfrac{\sin{\pi x}}{\pi x}\)
In either case, the value at \(x = 0\) is defined to be the limiting value:
\(\lim_{x\rightarrow 0}=\cfrac{\sin{ax}}{ax}=1, a\neq 0\)
sinc函数图像:

本文链接:https://cs.pynote.net/math/202210131/
-- EOF --
-- MORE --