-- TOC --
subderivative,或称subgradient,是更加一般化的derivative的概念。
In mathematics, the subderivative, subgradient, and subdifferential generalize the derivative to convex functions which are not necessarily differentiable. Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization.
凸优化领域的一个概念,凸函数存在一些不可微分的点,这些点可以采用subderivative。

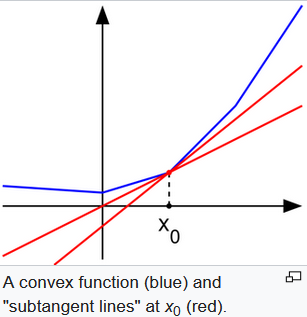
For example, the absolute value function \(f(x)=|x|\) is nondifferentiable when x=0. However, as seen in the graph in the above (where f(x) in blue has non-differentiable kinks similar to the absolute value function), for any x0 in the domain of the function one can draw a line which goes through the point (x0, f(x0)) and which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative (because the line is under the graph of f).
上图中,那两根红线的slope,都可以算作\(x_0\)的subderivative。
Consider the function \(f(x)=|x|\) which is convex. Then, the subdifferential at the origin is the interval \([−1, 1]\). The subdifferential at any point \(x0<0\) is the singleton set {−1}, while the subdifferential at any point \(x0>0\) is the singleton set {1}.
凸函数不可导点的subderivative,是一个range。
我不是很确定对max函数求导是否属于subderivative,我看的学习资料,用词为
(sub)derivative,这是在暗示。
max函数定义如下:
\(f(x,y) = \max(x,y)\)
求导:
\(\cfrac{\partial f}{\partial x}=1(x\ge y)\)
\(\cfrac{\partial f}{\partial y}=1(x\le y)\)
1(...)这是个indicator function,它表示,如果满足括号中的条件,值为1,否则值为0。
Hint: the SVM loss function is not strictly speaking differentiable
max函数确定不是那种严格可导的函数。在有max的loss function中,比如svm,做gradient check,有的时候会失败,就可能是这个原因。
本文链接:https://cs.pynote.net/math/202210201/
-- EOF --
-- MORE --