-- TOC --
牛顿插值法的作用,是用多项式拟合曲线。所谓多项式拟合,就是只知道曲线上的一些点,不知道函数表达式,用多项式函数来拟合这条曲线。这种拟合计算,与现代部分人工智能算法联系紧密。
假设一直4个点的位置,我们可以通过列出线性方程组的方式,来求出一条经过这4个点的曲线。
设 \(y=ax^3+bx^2+cx+d\)
分别将4个点的值带入,得到4个只含abcd的方程,可解出abcd。
此时如果在增加1个点,重新做拟合,就要重新使用一个更高次的4次多项式方程,解出abcde这5个系数。
这个方法的计算量太大,对于当时的行星观察而言,动辄几万个点;而且,每新增一个点,可能就需要重新拟合计算。
格雷戈里和牛顿不约而同地、独立地给出了可以解决上述两个问题的、求解多项式曲线的方法。由于牛顿太有名,因此这个方法被称为牛顿插值法。
假设有4个已知的点:\((x_0,y_0),(x_1,y_1),(x_2,y_2),(x_3,y_3)\)
从第1个点\((x_0,y_0)\)开始计算,此时只有1个点,经过这一个点的,就是一个常数函数:
\(f(x) = f_0(x) = f_0(x_0) = y_0\)
增加1个点,现在有2个点\((x_0,y_0),(x_1,y_1)\),构造函数如下:
\(f(x) = f_1(x) = f_0(x) + b_1(x-x_0)\)
这样构造函数,保证了此函数经过前面已经计算过的第1个点,带入\(x=x_0\)后,\(f_1(x_0) = f_0(x_0)\),第二个函数与第一个就成了一样的。这个构造函数经过前面的点的技巧是牛顿插值法的关键。
可解出 \(b_1 = \cfrac{f(x_1)-f(x_0)}{x_1-x_0} = \cfrac{y_1-y_0}{x_1-x_0}\)
再增加1个点,现在有3个点\((x_0,y_0),(x_1,y_1),(x_2,y_2)\),构造函数如下:
\(f(x) = f_2(x) = f_1(x) + b_2(x-x_1)(x-x_0)\)
这样构造函数,保证了新函数一定经过前面已经计算过的两个点。
可解出 \(b_2 = \cfrac{\frac{y_2-y_1}{x_2-x_1}-\frac{y_1-y_0}{x_1-x_0}}{x_2-x_0}\)
看到点规律了嘛...
再增加1个点,现在有4个点\((x_0,y_0),(x_1,y_1),(x_2,y_2),(x_3,y_3)\),构造函数:
\(f(x) = f_3(x) = f_2(x) + b_3(x-x_2)(x-x_1)(x-x_0)\)
肯定可以解出\(b_3\),由于\(b_3\)的表达式有点复杂,这里引入一种新的标记方法差商:
\(f(x_0) = f[x_0]\)
\(b_1 = \cfrac{y_1-y_0}{x_1-x_0} = f[x_0,x_1]\)
\(b_2 = \cfrac{f[x_1,x_2]-f[x_0-x_1]}{x_2-x_0} = f[x_0,x_1,x_2]\)
\(b_3 = \cfrac{f[x_1,x_2,x_3]-f[x_0,x_1,x_2]}{x_3-x_0} = f[x_0,x_1,x_2,x_3]\)
这里就是降低计算量的关键:

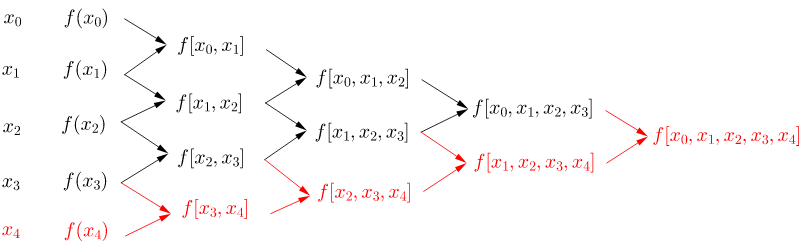
差商的这种层层递进的数值关系,使得每增加一个新的点,只需要计算与新增的这个点的相关的差商,其它已经计算出来的差商保持不变。
最后,牛顿插值法的计算公式:
$$f(x)=f[x_0] + f[x_0,x_1](x-x_0) + \cdots + f[x_0,x_1,...,x_n]\Pi_{k=0}^{n-1}(x-x_k)$$
笔记做到这里,由于有一点人工智能神经网络算法的背景,我感觉牛顿插值法是否存在过拟合的问题。因为,计算出来的曲线,必然会严格经过所有的已知的点。
本文链接:https://cs.pynote.net/math/202208292/
-- EOF --
-- MORE --