微分中值定理，洛必达法则

Last Updated: 2024-05-26 11:33:57 Sunday

-- TOC --

费马引理
驻点（Stationary Point）
罗尔中值定理
拉格朗日中值定理
柯西中值定理
洛必达法则

费马引理

定理，设函数$f(x)$在点$x_0$的某领域$U(x_0)$内有定义，且在$x_0$点可导，如果$\forall x\in U(x_0)$，有：

$f(x)\le f(x_0)$（或$f(x)\ge f(x_0)$）

那么，$f'(x_0)=0$

可导函数的极值点的导数为0。

驻点（Stationary Point）

导数为0的点，称为驻点。

导数可以理解为速度（变化率或敏感度），所以$f'(x_0)=0$意味着在$x_0$点的速度为 0，也就是停驻的意思。所以满足导数为 0 的点也称为驻点（stationary points）。

驻点不一定是极值点，比如$y=x^3$在$x=0$这个点。

极值点也不一定是驻点，因为有可能那个点不可导。

罗尔中值定理

如果函数$y=f(x)$满足：

在闭区间$[a,b]$上连续；
在开区间$(a,b)$上可导；(有可能在端点处单侧不可导，比如圆的一半作为函数，端点处导数无穷大)
$f(a)=f(b)$

那么，$\exist\xi\in(a,b)$，使得$f'(\xi)=0$

数学就像编程一样，定理或接口函数，越一般化越好，限制条件越少越好。如果闭区间可导，显然这个开区间也可到，但闭区间可导就要更严格一点点。

拉格朗日中值定理

如果函数$y=f(x)$满足：

在闭区间$[a,b]$上连续；
在开区间$(a,b)$上可导；

那么，$\exist\xi\in(a,b)$，使得$f'(\xi)=\cfrac{f(b)-f(a)}{b-a}$

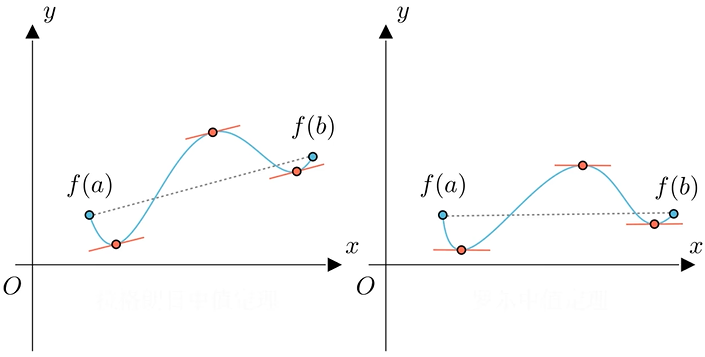
罗尔中值定理，在拉格朗日中值定理的描述下，成了一个特例，但却可以用来证明拉格朗日中值定理。

$zhongzhi_dingli.png$

$\cfrac{f(b)-f(a)}{b-a}$可以理解为物体在a和b两个时刻之间移动的平均速度。

柯西中值定理

如果函数$f(x)$和$g(x)$满足：

在闭区间$[a,b]$上连续；
在开区间$(a,b)$上可导；
$\forall x\in(a,b),g'(x)\neq0$

那么，$\exist\xi\in(a,b)$，使得$\cfrac{f(b)-f(a)}{g(b)-g(a)}=\cfrac{f'(\xi)}{g'(\xi)}$

还是用平均速度来直观的理解柯西中值定理，此时，速度是一个二维向量，物体在平面的两个方向上都有速度。当物体在平面上，从一个点移动到另一个点的过程中，这中间一定有一个点的速度，等于此过程的平均速度。

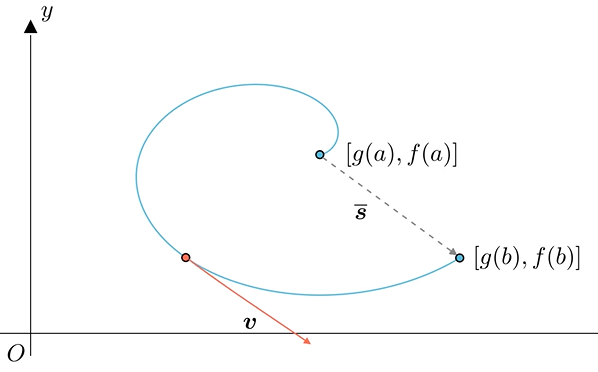
$kexi_zhongzhi_dingli.png$

如果推广到N维空间的移动，应该也是OK的，只是除法只能表达二维。

洛必达法则

极限定义导数，导数又反过来协助求解极限。

$\cfrac{0}{0}$ 型

$\lim_{x\rightarrow a}f(x)=\lim_{x\rightarrow a}g(x)=0$
在某$\mathring{U}(a)$内，$f'(x)$和$g'(x)$都存在，且$g'(x)\neq0$
$\lim_{x\rightarrow a}\cfrac{f'(x)}{g'(x)}$ 存在或无穷大

则： $\lim_{x\rightarrow a}\cfrac{f(x)}{g(x)}=\lim_{x\rightarrow a}\cfrac{f'(x)}{g'(x)}$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}g(x)=0$
当$x\gt N,N\in Z^+$，$f'(x)$和$g'(x)$都存在，且$g'(x)\neq0$
$\lim_{x\rightarrow +\infty}\cfrac{f'(x)}{g'(x)}$ 存在或无穷大

则： $\lim_{x\rightarrow +\infty}\cfrac{f(x)}{g(x)}=\lim_{x\rightarrow +\infty}\cfrac{f'(x)}{g'(x)}$

当$x\rightarrow -\infty$时也可以，以上条件做相应的修改。

直觉推导

当$f(x),g(x)$在$x \rightarrow a$的时候，有：

$f(x) \approx f(a) + f'(a)(x-a)$

$g(x) \approx g(a) + g'(a)(x-a)$

由于$f(a)=0,g(a)=0$，因此上下做个除法就得到了洛必达法则。

$\cfrac{\infty}{\infty}$ 型

$\lim_{x\rightarrow a}f(x)=\lim_{x\rightarrow a}g(x)=\pm\infty$
在某$\mathring{U}(a)$内，$f'(x)$和$g'(x)$都存在，且$g'(x)\neq0$
$\lim_{x\rightarrow a}\cfrac{f'(x)}{g'(x)}$ 存在或无穷大

则： $\lim_{x\rightarrow a}\cfrac{f(x)}{g(x)}=\lim_{x\rightarrow a}\cfrac{f'(x)}{g'(x)}$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}g(x)=\pm\infty$
当$x\gt N,N\in Z^+$，$f'(x)$和$g'(x)$都存在，且$g'(x)\neq0$
$\lim_{x\rightarrow +\infty}\cfrac{f'(x)}{g'(x)}$ 存在或无穷大

则： $\lim_{x\rightarrow +\infty}\cfrac{f(x)}{g(x)}=\lim_{x\rightarrow +\infty}\cfrac{f'(x)}{g'(x)}$

当$x\rightarrow -\infty$时也可以，以上条件做响应的修改。

以上条件都要求求导之后的极限存在，如果求导之后的极限不存在，并不能说明原式子的极限也不存在，要换个方法计算。洛必达法则不是万能！

本文链接：https://cs.pynote.net/math/202208091/

-- EOF --

-- MORE --