Last Updated: 2024-02-29 08:27:41 Thursday
-- TOC --
有一个经典的概率问题:N个人在一起开party,问这N个人中,至少有2个人生日相同的概率是多少?(N>=2,不考虑2月29的情况,不考虑润年,不考虑双胞胎。)
参考:《统计与概率》学习笔记
至少有2个人生日相同的概率,与完全没有人生日相同的概率,形成互补,而后者更容易计算。
# N=2,生日相同的概率:
>>> 1 - 364/365
0.002739726027397249
# N=3,至少2人生日相同的概率:
>>> 1 - (364/365)*(363/365)
0.008204165884781345
# N=4,至少2人生日相同的概率:
>>> 1 - (364/365)*(363/365)*(362/365)
0.016355912466550215
Hash表的碰撞概率(至少2个key经过hash计算,得到的positon一样),与此问题类似(假设input是完全随机的)。N个完全随机的key,通过hash计算position,共有M个position,碰撞的概率如何计算。就如N个人,每个人都有个随机的生日,共365种可能,碰撞的概率一样。
本文讨论完全随机的key,hash函数能够让key均匀分布!
我们写一段代码来方便计算:
def hash_collision_p(N, M):
q = 1
for i in range(1,N):
q *= (M-i)/M
return 1-q
测试:
>>> hash_collision_p(2,365)
0.002739726027397249
>>> hash_collision_p(4,365)
0.016355912466550215
碰撞概率的高,远超想象:
>>> hash_collision_p(20,365)
0.41143838358058027
>>> hash_collision_p(24,365)
0.538344257914529
>>> hash_collision_p(28,365)
0.6544614723423995
>>> hash_collsion_p(32,365)
0.7533475278503208
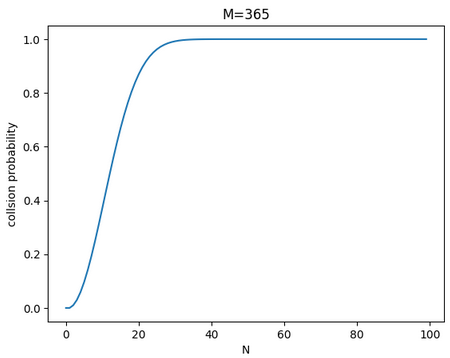
当N=32人时,生日相同的概率,就已经超过75%了!
画个图:

对于一个有10000个Position的Hash表:
>>> hash_collsion_p(120,10000)
0.5117175336118225
>>> hash_collsion_p(160,10000)
0.7216336576276512
>>> hash_collsion_p(200,10000)
0.8651196385197777
所以,不要以为自己的Hash表容量很大,key数量少,就可以不考虑碰撞,或者认为碰撞的概率很低。这是错误的观点!从上述数据来分析,如果要将碰撞概率控制在很小的水平上,position的数量需要比key的数量至少大20倍以上!
Load Factor
Hash表中元素个数与位置数的比值,即\(\alpha=\cfrac{N}{M}\)。如果采用open chaining方式处理collision,它同时也是Expected Length of Chain。
Rehashing
Rehasing是一个动作。比如,当碰撞的概率超过设定的阈值,或者说,当Load Factor超过阈值,扩大位置数,但要对所有元素进行Rehasing。就是新创建一个容量更大的Hash Table,然后将所有元素全部重新添加进去,此过程会重新计算每个元素的hash值,因此称为Rehashing。
Bucket
Bucket就是对本文Position的另一个称呼,编程语言中似乎更喜欢用Bucket这个词。
Open Chaining
在Hash表的实现中,一般都会采用Linked-List方式来处理冲突,这个List被称为Collision Chain,或Open Chainning。这个链表越长,性能越差。理论上Hash表(采用Linked-List处理冲突)的查询Big-Oh是\(O(N)\),这是极端情况下,即Worst Case,由查询Collision Chain造成的。实际上,Hash表的分析更应该使用Expected Time Complexity:
Unsuccessful查询时间复杂度,这就是我们喜闻乐见的\(\Theta(1+\alpha)\),必须查询到end of chain。Successful的查询时间复杂度,分析如下:Hash表中有N个元素,Successful查询可能查询这N个元素中的任何一个,假设查询第\(ith\)个元素,此时有\(N-i\)个元素在\(ith\)元素后面加入Hash表,在使用open chaining时,有\(\cfrac{N-i}{M}\)个元素可能出现在\(ith\)元素的前面,因此查询到\(ith\)元素的时间为\(1+\cfrac{N-i}{M}\),查询N个元素中任意一个的概率相同,所以,Expected时间复杂度为\(\cfrac{1}{N}\cdot\sum\limits_{i=1}^N\left(1+\cfrac{N-i}{M}\right)=1+\cfrac{\alpha}{2}-\cfrac{a}{2N}\)。
参考:理解算法分析
当然也可以不用Linked-List来处理Hash Table的冲突,可选项还有Red Black Tree等。
Closed Chaining
Open Chaining的一个缺点,空间利用率有点低,必须为chain申请额外的空间,同时hash table本身还有大量的空间没有被利用起来(看看前文计算碰撞概率,就知道hash table内部的剩余空间是很多的)。
Closed Chaining方案,就是把一个个chain隐藏在hash table内部,去充分利用hash table已有的空间。Hash函数不再仅仅计算一个position,而是计算出一个位置序列,当前面的position已经被占用时,就尝试后一个position,直到找到一个空位置为止。最简单的位置序列,就是前一个位置+1。Closed Chaining是Python采用的方案。
本文链接:https://cs.pynote.net/math/202306131/
-- EOF --
-- MORE --