-- TOC --
曲率定义圆的弯曲程度:
\(K = \cfrac{1}{r}\)
曲率K被定义为圆半径r的倒数。
半径越小,曲率越大;半径越大,曲率越小。
当半径趋向无穷大的时候:
\(K = \lim_{r\rightarrow\infty}\cfrac{1}{r} = 0\)
这非常符合直觉。古时候,人们认为地球是平的,就是因为相对人而言,地球的半径太大了。
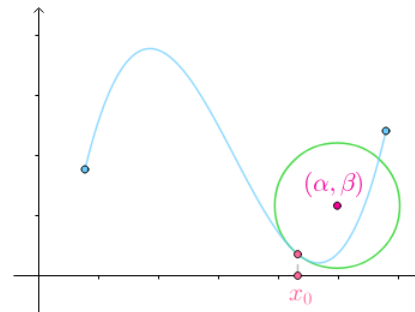
将圆的曲率扩展到曲线,曲线上任一点的密切圆(osculating circle),是对这一点附近曲线的最佳圆近似,密切圆的曲率,就是曲线在这一点的曲率。
在曲线较为平坦的地方,密切圆半径很大,较为弯曲的地方,密切圆半径就较小。
曲线上这一点的切线,同时也是密切圆的切线。
已知函数\(f(x)\)在\(x_0\)点有二阶导数\(f''(x_0)\),且\(f''(x_0)\neq0\),则此点有密切圆存在,其半径为:
\(r = \cfrac{(1+(f'(x_0))^2)^{\frac{3}{2}}}{|f''(x_0)|}\)
曲率为:
\(K = \cfrac{1}{r} = \cfrac{|f''(x_0)|}{(1+(f'(x_0))^2)^{\frac{3}{2}}}\)
\(f''(x_0)=0\),则\(x_0\)点是拐点,不存在密切圆。
所以密切圆也称为曲线的曲率圆,半径r称为曲率半径。

如果要画出密切圆,还需要计算出圆心在哪里......有半径,切线的垂直线指明了半径方向....
$$\begin{cases} \alpha = x_0 - \cfrac{f'(x_0)(1+(f'(x_0))^2)}{f''(x_0)}\\ \beta = f(x_0) + \cfrac{1+(f'(x_0))^2)}{f''(x_0)}\\ \end{cases}$$
此圆心,也称为曲率中心。
当\(x_0\)开始移动,会得到一条密切圆圆心轨迹\(g(x)\),这条轨迹称为渐曲线。\(f(x)\)也被称为渐伸线。
本文链接:https://cs.pynote.net/math/202209023/
-- EOF --
-- MORE --