Last Updated: 2024-04-14 13:38:30 Sunday
-- TOC --
本文总结几种求解递归等式的方法,主要用于分析算法的复杂度,从求解著名的Fabonacci数列的通项开始.....
在分析算法的时间复杂度时,如果算法实现没有递归,整个计算是比较直接的。而一旦用了递归,计算就不那么容易了...
线性递归
Linear Recursive Relationship: A linear recurrence, also known as a linear recurrence relation or linear difference equation, is a mathematical equation that expresses a sequence of numbers, where
each term is a linear combination of the previous terms. In other words, it defines the nth term of a sequence in terms of the previous terms.
递归算法的时间复杂度的计算,大多是求解线性递归等式。虽然是线性,但由于有各种不同形态的线性递归,求解也方法不尽相同...甚至有一些难以解出来...
非线性递归
某些计算Expected Time Complexity的场景,容易出现非线性的Recurrence!比如对QuickSort算法进行Expected Case分析时。
著名的Fabonacci数列:0,1,1,2,3,5,8,13...是个线性递归数列(linear recurrence)。
\(\begin{cases} f(0)=0,\ n=0 \\ f(1)=1,\ n=1 \\ f(n)=f(n-1)+f(n-2),\ n>1 \\ \end{cases}\)
CS430的教授说,这个方法叫做
method of characteristic equation,还不明白这是啥,但整个解法是明白了的。据说这个方法是模仿了解线性微分方程组的方法。这个方法比《数学女孩1》中使用generating function的方法要好一些。
设\(f(n)=ak^n,\ a\neq 0\),
如果这里没有a这个系数,是不对的,虽然后面的计算将这个系数约掉了,但不等于它不存在,仅仅只是约掉而已,并没有把a解出来,因此后面虽然计算出了k的非0解,但由于没有找到a,因此并不是最后的解答。至于为什么要这样假设,数学嘛,先猜后证明也可以,很多时候需要一点直觉...
由\(ak^n=ak^{n-1}+ak^{n-2}\),整理后可得:
\(k^2-k-1=0\),解出这个quadratic(这就是characteristic equation):
\(k=\cfrac{1\pm \sqrt{5}}{2}\)
此时,改写\(f(n)=a_1k_1^n+a_2k_2^n\)
这一步很tricky!前面的计算,没有算出a,只算出来了两个k。仅使用任何一个k计算,在f(0)时,a只能=0,这与前面假设不符。这里的改写,相当于把两个k都用上,两个k,两个等式,将两个等式相加,依然是等式。换一个角度看,这种新的写法,就是两个k的线性组合。
根据两个初始条件\(f(0)=0,f(1)=1\),得到:
\(\begin{cases} a_1+a_2=0 \\ a_1\cdot\cfrac{1+\sqrt{5}}{2} + a_2\cdot\cfrac{1-\sqrt{5}}{2}=1 \\ \end{cases}\)
解出\(a_1=\cfrac{1}{\sqrt{5}},\ a_2=-\cfrac{1}{\sqrt{5}}\)
两个k,两个initial conditions, 刚好解出两个系数。
最后,得到Fabonacci数列的通项:
\(f(n)=\cfrac{1}{\sqrt{5}}\cdot\left(\left(\cfrac{1+\sqrt{5}}{2}\right)^n-\left(\cfrac{1-\sqrt{5}}{2}\right)^n\right)\)
可以看出,Fabonacci数列本质上是两个等比数列(Geometric Sequence/Series)的各项和......还是,任何数列都可以被分解成多个等比数列的和?
\(a_n=c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}\)
设 \(a_n=cr^n\)
带入后,得到的方程,有k个root。
当这k个root都不同时,可完全参考上述方法计算,那个很tricky的步骤为:
\(a_n=t_1r_1^n+t_2r_2^n+...+t_kr_k^n\)
假设k个root中,r1是重复m次的root,那个很tricky的步骤,就要写成下面这样:
\(a_n=t_1r_1^n+t_2nr_1^n+...+t_mn^{m-1}r_1^n+...\)
root数超过2时,基本都是很难解的方程。
所谓inhomogeneous,就是指递归公式中,有一些其它的项存在:
\(a_n=c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}+f(n)\)
此时,
\(a_n=t_1k_1^n+t_2k_2^n+...+t_kk_k^n+g(n)\)
\(g(n)\)与\(f(n)\)的形式相同,都是n的m次项,只是系数不同。
计算过程为:先计算homogeneous部分,在tricky步骤,增加\(g(n)\),用更多的initial condition列出足够的方程求解。请见下一节的示例。
这个假设了一颗空树的高度为0,避免了-1。而很多其它文献假设空树的高度为-1,这样当只有一个root节点时,高度就是0。注意这个不同的细节,如果假设不同,解出来的通项系数是不同的,但结果一样。
\(\begin{cases} N_{0} = 0 \\ N_{1} = 1 \\ N_{h} = N_{h-1} + N_{h-2} + 1 \\ \end{cases}\)
现在用上文介绍的方法,解出\(N_{h}\)的通项,然后就可以直接一步根据h计算AVL树的最小节点数。算式很容易列出来,但,太难算了....我算了四五遍才得到如下:
\(N_h=\left(\cfrac{4+2\sqrt{5}}{5+\sqrt{5}}\right)\cdot\left(\cfrac{1+\sqrt{5}}{2}\right)^h + \left(\cfrac{1-\sqrt{5}}{5+\sqrt{5}}\right)\cdot\left(\cfrac{1-\sqrt{5}}{2}\right)^h - 1\)
用Python验证一下:
>>> round(c1*phi**0+c2*hphi**0+c3)
0
>>> round(c1*phi**1+c2*hphi**1+c3)
1
>>> round(c1*phi**2+c2*hphi**2+c3)
2
>>> round(c1*phi**3+c2*hphi**3+c3)
4
>>> round(c1*phi**4+c2*hphi**4+c3)
7
>>> round(c1*phi**5+c2*hphi**5+c3)
12
>>> round(c1*phi**6+c2*hphi**6+c3)
20
还有一种数学技术,叫做sequence operator,造出所谓的annihilator,来求解linear recurrence。其最后的解方程步骤,与本文的方法完全一样,只是前面有所不同。(见CS430的lecture 2 notes)
其实,空树高度为-1更符合一般情况!\(2^h\)表示最大叶子数。
这就是直接展开的意思,这种方法不用画图,相对比较简单。举个例子:
Solve the following recurrence:
$$\begin{cases} T(0)=1 \\ T(n)=4T(n-1)+2^n, n>0\end{cases}$$
Let's just unfold it:
$$\begin{aligned} T(n) &= 4T(n-1)+2^n \\ &= 4\left(4T(n-2)+2^{n-1}\right)+2^n \\ &= 4^2T(n-2)+2\cdot2^n+2^n \\ &= 4^2\left(4T(n-3)+2^{n-2}\right)+2\cdot2^n+2^n \\ &= 4^3T(n-3)+4\cdot2^n+2\cdot2^n+2^n \\ &= 4^n + 2^n\sum_{i=0}^{n-1}2^i \\ &= 4^n + 2^n(2^n-1) \\ &= 2\cdot4^n-2^n \end{aligned}$$
The complexity is \(\Theta(4^n)\).
二分查找 Binary Search 的递归也可以用unfold的方法直接解开:
$$T(n)=2\cdot T(n/2)+1$$
再来一个,Mergesort:
$$T(n)=2\cdot T(n/2) + n$$
这些都是直接unfold比较好计算的形式,基本上一目了然,形式上要么n-1,要么n/2...
有些非线性递归等式,也可以用unfolding的方法来解,如下两例:
$$\begin{aligned} T(n)&=\sqrt{n}\cdot T(\sqrt{n})+n \\ &=n^{\frac{1}{2}}(n^{\frac{1}{4}}T(n^{\frac{1}{4}})+n^{\frac{1}{2}})+n \\ &=n^{\frac{1}{2}+\frac{1}{4}}(n^{\frac{1}{8}}T(n^{\frac{1}{8}})+n^{\frac{1}{4}})+n+n \\ &=\Theta(n\log\log{n}) \\ \end{aligned}$$
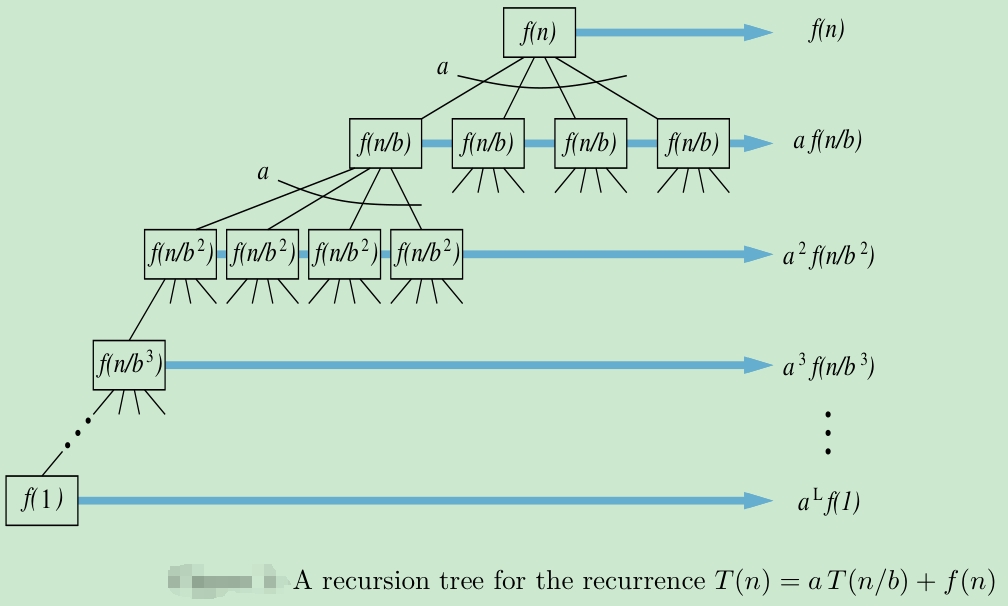
Master Theorem针对形如\(T(n)=aT(n/b)+f(n)\)这样的线性递归表达式,证明Master Theorem的方法,其实就是用画Recursive Tree的方法。

\(T(n)=f(n)+af(n/b)+a^2f(n/b^2)+...+a^hf(1)\)
\(h=\log_b{n}\)
\(f(1)=1\)
当\(af(n/b)=k\cdot f(n)\)时,存在下面3种情况:
当\(f(n)\)与\(af(n/b)\)没有这种Constant Factor的关系时,you are on your own,此时master theorem不适用。下面简单推一下:
\(T(n)=f(n)+kf(n)+k^2f(n)+...+k^hf(n)\)
这显然是个geometric series。还需要下面这个等式,就可以完整推导了:
\(a^hf(1)=k^hf(n)\)
Recursive Tree是更通用的方法,就是画出图形来直接证明计算,Master Theorem都能用它直接证明,不过在应用时也需要技巧。下面用两道题示例:
\(T(n)=T(n/3)+T(2n/3)+n\)
This uneven splitting method makes the tree lopsided, different leaves are at different levels, which are from \(\log_3{n}\) to \(\log_{3/2}{n}\). However, it's not hard to see that the nodes in any complete level (above any leaves) sum to \(n\). To derive an upper bound, we could overestimate \(T(n)\) by extending the tree down to the level of the deepest leaf, and get the upper bound \(O(n\log_{3/2}{n})\). Similarly, to derive a lower bound, we underestimate \(T(n)\) by counting only nodes in the tree up to the level of the shallowest leaf, and get the lower bound \(\Omega(n\log_3{n})\). So, we have \(n\log_3{n} \le T(n)\le n\log_{3/2}{n}\). Since these two bound differ by only a constant factor, we have \(T(n)=\Theta(n\log{n})\).
\(T(n)=T(n/5)+T(7n/10)+n\)
If draw out the recursive tree, it is a lopsided tree. At each level, we have \(n,9n/10,81n/100,...\), which is a descending geometric series. Whether if we overestimate by extending the tree down to the deepest level, or underestimate by counting only to the shallowest leaf, the sum of geometric series is dominated by the largest term. So, \(T(n)=\Theta(n)\).
本文链接:https://cs.pynote.net/math/202401251/
-- EOF --
-- MORE --