Last Updated: 2024-05-03 14:56:00 Friday
-- TOC --
逻辑的起点是概念,清晰地理解概念,才能开始有质量的理解和推导。本文的理解不一定严谨,也不一定对,是我自己的理解,我想尝试把一维向量和N维世界统一起来。
向量,即有大小,又有方向。
一维向量,有大小,但只有2个方向,正或负。
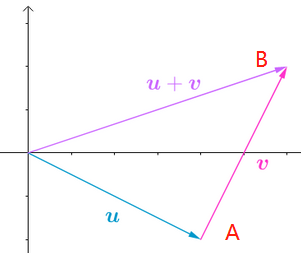
向量的大小,是它的长度;向量的方向,就是从起点到终点的方向。比如从A到B,可以表达为:\(\overrightarrow{AB}\)。
物理中不太在乎起点、终点具体在什么位置,而在数学中,始终把向量的起点放在原点\(O\)。
起点都在原点O,那\(\overrightarrow{AB}\)是什么意思?
我的理解:\(\overrightarrow{AB}\)这种有起点和终点,上面还带个箭头,是物理上习惯的表达,不是数学上的。数学上对向量的表达,就是单纯的行向量或列向量,因为起点总是在原点,也就可以将其省略了。
如果\(A=(x,y,z),B=(a,b,c)\),那么:
\(\overrightarrow{AB} = (a-x,b-y,c-z)\)
左边是物理上的表达,右边是数学上的表达。理解左边的向量,不要关心原点在哪里。而右边的向量,原点已经明确是原点。

上图的\(\overrightarrow{AB}\)就是\(v\),将A点移动到原点,才能与它的2个分量的值对应起来。
数学书上还存在一种用向量加法表达向量的方式,如下:
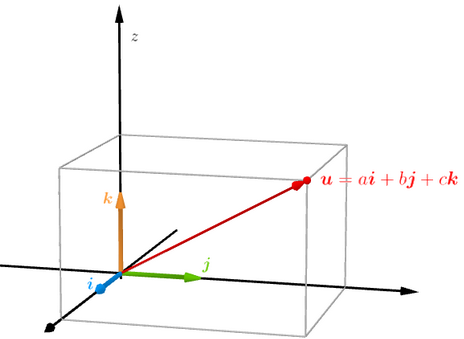
\((x,y,z) \iff u = xi+yj+zk\)
ijk分别是xyz三个坐标轴方向的单位向量。如下图所示:
数学上默认向量都是列向量,比如:
\(x=\begin{bmatrix} 1\\ 2\\ 3\end{bmatrix}\),它等价于\(x=(1,2,3)\)(x不是行向量哦,这样表达是为了节省空间)。
一维的情况,所有点都在x轴\(R\)上,每个点有1个分量,\(x\),长度是距离0点的距离,\(|x|=\sqrt{x^2}\)。
一维向量与标量是一样的,只是这两个名称分表代表了不同的范畴。
二维的情况,所有点都在xOy平面\(R^2\)上,每个点有2个分量,\((x_1,x_2)\),长度是2个分量平方开根号,\(|x|=\sqrt{x_1^2+x_2^2}\)。
三维的情况,所有点都在三维空间\(R^3\)中,每个点有3个分量,\((x_1,x_2,x_3)\),长度是\(|x|=\sqrt{x_1^2+x_2^2+x_3^2}\)。
......
N维的情况,所有点都在\(R^n\)高维空间中,每个点有n个分量,\((x_1,x_2,\cdots,x_n)\),长度是\(|x|=\sqrt{\Sigma_{i=1}^{n}x_i^2}\)。
每个分量的值,就是那个维度的坐标。
值就是坐标。
向量长度与数量的绝对值是统一的,有时向量长度使用\(||x||\)。
向量就是空间中的一个数,这个数本身具有大小和方向这两个属性。
如果我们将一维数据也纳入向量的范畴,那么:
向量就是一个数,其计算都满足交换律,结合律,分配率:
\(u+v = v+u\)
\((u+v)+w=u+(v+w)\)
\(k(u+v) = ku+kv\),其中\(k\)是标量。
以上算式,对于任意维度的向量而言,都满足,包括一维。
\(v-v=0\),这里的0是与v维度相同的0向量。
方向余弦组成的向量,就是向量所在方向的单位向量。
每个余弦的夹角,都是向量与轴的正方向的夹角。
二维空间方向余弦举例如下:
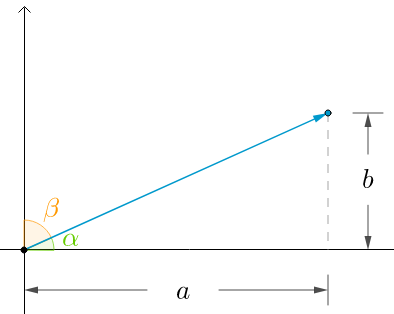
\((\cos\alpha,\cos\beta)=(\cfrac{a}{|u|},\cfrac{b}{|u|})=\cfrac{1}{|u|}(a,b)=\cfrac{u}{|u|}=e_u\)
因此,\((\cos\alpha)^2+(\cos\beta)^2=1\)
这个结论推广到\(R^n\)也一样成立。
对于一维空间R,\(\alpha\)角度或0或\(\pi\),其\(\cos\)值,或1或-1。而\(\cos\beta=0\),因为\(b=0\),同样满足上述结论。
另外,\(\alpha+\beta=\cfrac{\pi}{2}\),这是一种常见的表达方式:\(\begin{bmatrix} \cos\alpha\\ \sin\alpha\end{bmatrix}\)
设\(a=(a_1,a_2),b=(b_1,b_2)\),那么,
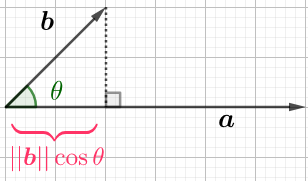
\(a\cdot b=a_1 b_1 + a_2 b_2=|a||b|\cos\theta\)
同维度分量相乘,然后相加,结果是一个标量。
N维向量的点积也是如此定义。
一维向量只有一个分量,两个数相乘,还是一个数,依然符合点积的定义。
所以,普通乘法实际上是向量的点积在一维情况下的特例。
乘法满足交换律,结合律,以及分配率:
\(a\cdot b=b\cdot a\)
\((\lambda a)\cdot b=\lambda(a\cdot b)\),\(\lambda\)是个标量
\(a\cdot(b+c)=a\cdot b + a\cdot c\)
一维向量的\((ab)c=a(bc)\)成了一种特例,标量和向量在一维空间统一了。
向量乘法(点积)的真正含义
向量的长度用点积来表达:\(|x|=\sqrt{x\cdot x}\)
点积,dot product,还有个名称,内积,inner product。执行点积后,方向消失。
两个向量\(a,b\),其夹角\(\theta\),
\(\cos\theta=\cfrac{a\cdot b}{|a||b|}\)
规定向量夹角的区间为\([0,\pi]\),在此区间,\(\cos\)函数具有反函数,因此可以很优雅的将余弦值与夹角等价起来。(这也是选择余弦的原因吧...)
两单位向量点积的结果,是这两个单位向量夹角的余弦。
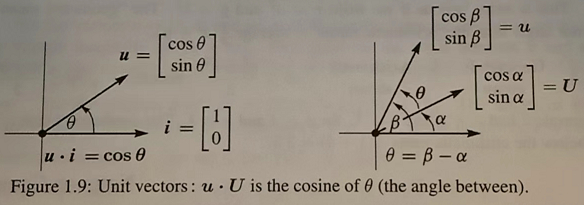
在一维情况下,两向量一定都在x轴上,夹角只有0或\(\pi\),按上式计算,值只有1或-1,完美对应。
当量向量夹角为90度时,夹角余弦等于0(点积为0即可),此时我们说两向量正交(perpendicular vector)。
而平行表示,夹角为0位\(\pi\),都算作平行向量。
在N维空间,与某一向量正交或平行的向量,无穷多。比如三维空间可以一个面(plane)与某个向量垂直。
零向量也有维度,N维空间零向量,就是N个值为0的分量。
零向量的位置在原点。
零向量的长度为0。
零向量的方向任意。因此,零向量与任意其它向量都同时平行和正交。
通过画出三维空间,遵循右手法则:
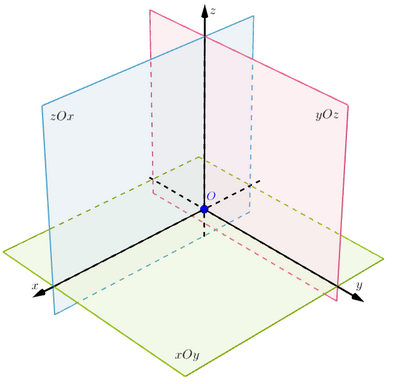
右手大拇指为z,其它4根手指指向x,手臂为y。
二维平面中,一条直线方程的一般形式,与三维空间中,一个平面的一般形式,是和谐和美好的:
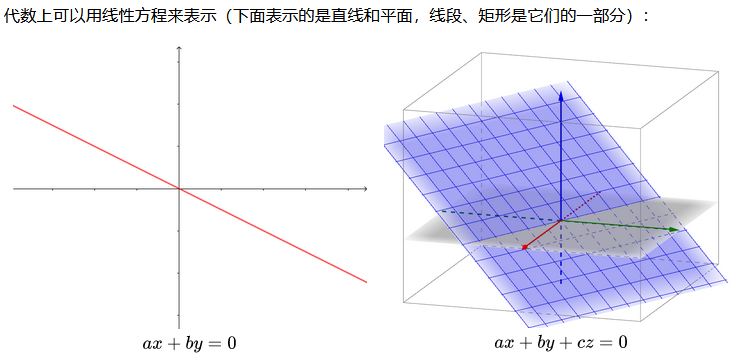
上图的线和面都经过了原点,因为都=0,即没有bias。
宇宙从零维空间开始。零维空间,只有1个点,其它什么没有,是宇宙大爆炸之前的奇点状态。
数学从一维空间开始。在一维空间,有线(line)。x轴上的每个点,都与原点连成一条线。一维空间只有这一条线。
在二维空间,有线也有面(plane)。xy平面上的每个点,都与原点连成一条线,xy平面上有无数条这样的线,但xy平面空间,只有一个平面。
在三维空间,有线,有面,也有空间(space)。xyz空间中的每个点,都与原点连成一条线,这样的线有无穷多。xyz空间中的任意两条独立的线,组成一个平面,这样的平面有无穷多。xyz只有一个空间。
在高维空间中,有线,有面,有子空间(hyperplane,subspace)。依然有,每个点与原点连成一条线,两条独立的线形成一个面,三条独立的线形成一个子空间......
这是线性代数的核心概念。
两个向量\(v,w\),两个标量\(a,b\),
\(av+bw\)就是线性组合。
如果\(v\)与\(w\)不共线,即不在同一条线上,这两个向量就是相互独立的,independent;如果共线,即在一条线上,只是与原点的距离可能不相同,这两个向量就是相关联的,dependent。
\(av\),是一条线,经过原点;随着a的变化,这条线可以表达v方向(正负)的任意向量,填满整条无穷延伸的线。
\(av+bw\),是一个面,经过原点(假设向量都independent);随着a和b的变化,填满整个平面。
\(av+bw+cu\),是一个三维空间,经过原点(假设向量都independent);...,填满整个空间。
\(av+bw+cu+dn\),是一个四维空间,经过原点(假设向量都independent);...,填满整个四维空间。
......
可以很容易的想象,如果是两个dependent的vector,在线性组合的时候,跟只有其中任意一个vector没有区别,这两个dependent的vector,只有一个方向,只有一条line,并不能组成plane。
线性代数可以教你构建一幅N维空间的mental picture!
在线性代数中,矩阵乘向量的表达式随处可见,如:\(Ax=b\),我们可以有多种不同的视角来解释这个表达式。
矩阵A列向量的线性组合。
\(A=(a_1,a_2,...,a_n)\),\(a_i\)是列向量,
\(x=(x_1,x_2,...,x_n)\)
\(Ax=a_1 x_1+a_2 x_2+\cdots+a_n x_n=b\)
列视角看到的,是A的所有column的一个线性组合,x是组合所用的系数,组合的结果是向量b。
矩阵A行向量与x的点积。
A中行向量与x的点积的表达式,是一组hyperplane方程(每个维度只有一个线性分量),所有的这些hyperplane交于一个点x,这个点x能够满足所有方程。
A的所有列向量,都视作变化后的各个轴的方向以及缩放程度,从左到右,xyz...
左乘x,矩阵A作用于x,用旋转和缩放标准坐标系 到 A列向量确定的新坐标系的方式,旋转缩放x。
这叫做线性变换,无论是变换前的向量,还是变换后的向量,都是以标准坐标系(N维笛卡尔坐标系)为参考。
用旋转来观察\(\begin{bmatrix}2&-1\\1&4\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}=\begin{bmatrix}1\\5\end{bmatrix}\)
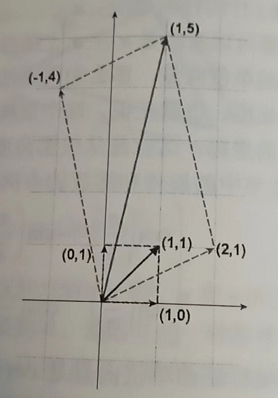
更多例子:
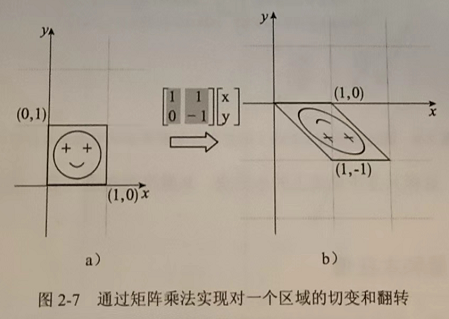
仿射变换,Affine Transformation
下面这个case,可以这样表达:\(\begin{bmatrix}1&1&1\\0&-1&2\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}\)
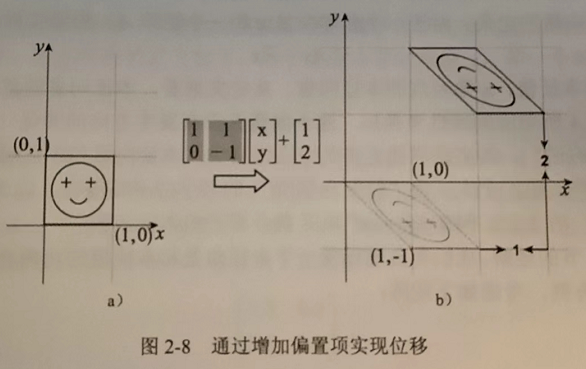
从旋转视角理解单位矩阵\(I\)乘任何向量,向量都不变,因为\(I\)就是标准坐标系。
矩阵乘向量再加上一个偏移,可以合并成一个计算:
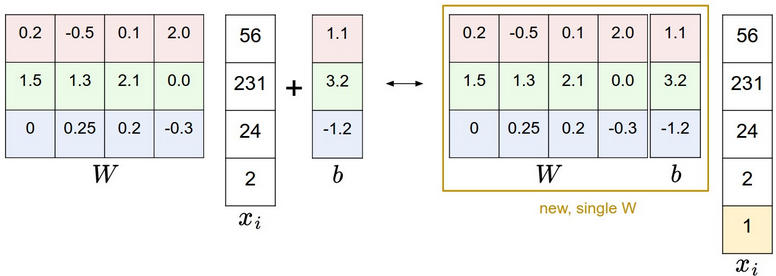
形如 \(y=Ax+b\) ,一个线性变换加上一个偏移,就叫做仿射变换!
仿字应该是affine的音译。
我们常用的向量间的L1/L2距离,属于这个范畴:
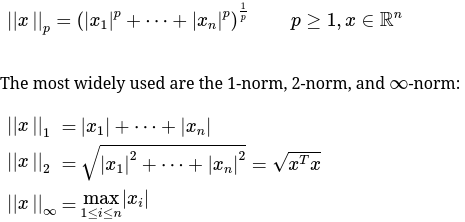
The 2-norm is sometimes called the
Euclidean vector norm, because \(||x−y||_2\) yields the Euclidean distance between any two vectors \(x,y\in R^n\). The 1-norm is also called thetaxicab metric(sometimesManhattan metric) since the distance of two points can be viewed as the distance a taxi would travel on a city (horizontal and vertical movements).
将L2 vector norm推广到matrix上,就是Frobenius Norm:
\(F=\sqrt{\sum\limits_{i=1}^n\sum\limits_{j=1}^m a_{ij}^2}=\sqrt{Tr(A^TA)}\)
这个norm计算,可用来判断两个matrix是否算是相等的,自己设个精度:
assert np.linalg.norm(dists2-dists1,ord='fro') < 0.000001
assert np.linalg.norm(dists1-dists0,ord='fro') < 0.000001
这是在cs231n课程的assignment1中学到的方法。
假设有两个矩阵\(A_{m\times n}\)和\(B_{k\times n}\),要计算得到一个矩阵\(C_{k\times m}\),其中\(C_{ij}\)表示\(B\)的第\(i\)行与\(A\)的第\(j\)行的L2距离。
计算方法有多种,可以2个循环,1个循环,或没有循环。
本文总结的超快的方法,没有循环。
数学原理:
\(||X - Y||\\ = \sqrt{(x_0-y_0)^2+(x_1-y_1)^2+\cdots+(x_n-y_n)^2}\\ = \sqrt{(x_0^2+x_1^2+\cdots+x_n^2)+(y_0^2+y_1^2+\cdots+y_n^2)-2(x_0y_0+x_1y_1+\cdots+x_ny_n)}\)
然后,我们可以构造矩阵,以没有循环的方式来计算上诉问题。下面用代码表示:
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
a = np.reshape(np.sum(X**2,axis=1),(num_test,1)) @ np.ones((1,num_train))
b = self.X_train.T
b = np.ones((num_test,1)) @ np.reshape(np.sum(b**2,axis=0),(1,num_train))
dists = np.sqrt(a + b - 2*(X@self.X_train.T))
return dists
下面是计算速度比较,分别与2个循环,1个循环比较:
Two loop version took 59.844741 seconds
One loop version took 37.532001 seconds
No loop version took 0.933600 seconds
Nice...(如果是AMD芯片,有可能出现one loop用时比two loops更多的情况)
本文链接:https://cs.pynote.net/math/202209061/
-- EOF --
-- MORE --