Last Updated: 2024-01-02 11:09:39 Tuesday
-- TOC --
当人类第一次抬头仰望星空,距离揭示宇宙奥秘就只有一步之遥。这句话是刘慈欣写的,他的意思应该是,人类文明对于整个宇宙来说,只是微不足道的一瞬间,另一层含义是,人类还是能够解开宇宙的奥秘的,这至少是一种期许。
这个问题就像为什么是十进制一样,就是因为人类自身和地球宇宙的特性。
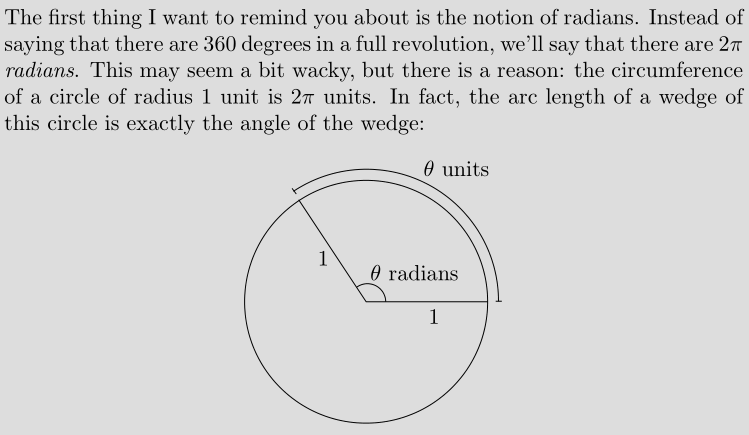
角度的出现,是源于对圆周运动的观察。这个世界上最大最显眼的圆周运动就是地球围绕太阳的转动,就算我们现代人知道地心说是错误的,可是以我们的尺度来看,抬起头观察到的是太阳在做圆周运动。作为观察者,我们也非常自然的,以我们自己为中心,开始计算太阳相对我们的移动,这就开始出现了角度。
古代人类就有黄道十二宫的说法,其实就是地球围绕太阳转动,人类在地球上看到天上的星星仿佛是固定在遥远的天幕上的。在遥远的古代,那个时候可是迷人的满天繁星呀!晚上吃跑了就躺在户外看星星,是否就像我们现在吃饱了打开电脑看片一样.....地球上的我们就像看走马灯一样,随着地球的公转,在特定的时间看到特定的星座。古人发现了这个规律,并且以星座为参照物,近似得出循环周期为360天(一个白昼为一天,当相同星座在相同位置出现时,便能够得到经过的天数),这就是一年。因此,天空就被等分成了360份,也就是圆被等分成了360份。
虽然后来古人慢慢发现了一年实际上是365天,但是因为360度已经成为习惯,并且非常好计算,所以就被保留了下来。
三角函数应该如何定义?
以前我一直是通过勾股定理来记忆三角函数,勾三股四玄五,正弦就是角的对边(opposite)比上斜边(hypotenuse),余弦就是邻边(adjacent)比上斜边,通过这样的记忆,还能够很容易的记住 \(\sin^2\alpha + \cos^2\alpha = 1\) 这样的公式。
这种记忆方法有缺陷。当我们要求的角度大于90度的时候,已经无法用直观的直角三角形的方法来计算正弦和余弦。促使我去思考这个问题的动力,还来自一个简单的问题:为什么 \(\sin180^\circ=0\) ?(因为180度已经无法用三角形来表示了)
很无聊吧!老男孩学数学总喜欢去想更深层次的原理。不记得中学时老师教过没有,也许教过但是已经遗忘,或者是我从来都把数学当成了计算(算术),觉得只能计算好了就把数学学好了,而忽略了对原理的深刻理解。这种理解不是能够通过计算练习就可以达到的。
计算机也不仅仅是编程,编程只是手段...
后来发现了一个解:在笛卡尔坐标轴上画一个半径为1的单位圆,用这个圆来解释并定义三角函数!
假设已经有了这样一个圆,圆内有一条半径线按逆时针方向运动,所要计算的角度为这条半径线与x轴正方向之间形成的角度。当这条半径线处于第一象限时,也就是要计算正弦余弦的角度还在90度以内;当这条半径线逆时针移动到第二象限,这时的角度在90度到180度之间,计算方法永远都是将这条半径线映射到y轴,取y轴这一段的值,除以半径长度,得到角度正弦值。余弦值的计算一样,将半径线映射到x轴,用这个值去除以半径。由于半径为1,所以这个映射之后得到的值,就是正弦和余弦的值。

当半径线在第二象限时,映射到y轴的值为正,所有正弦值为正,映射到x轴的值为负,所有余弦的值为负。用这个方法,还可以很好的记忆三角函数的诱导公式。诱导公式的要诀是:奇变偶不变,符号看象限!这个符号看象限,看得就是在第几象限,正弦和余弦的值是正还是负。用这种映射的方法,可以非常清晰的判断,正弦在1,2象限为正,3,4象限为负,余弦在1,4象限为正,在2,3象限为负。
上图也说明了使用弧度的原因,圆周(circumference)的长度公式为\(2\pi r\),\(2\pi\)就代表了360度。
诱导公式是指三角函数中将角度比较大的三角函数利用圆的周期性,转换为角度比较小的三角函数的公式。
三角函数都是周期函数,而且都有2π周期(tan和cot的最小周期是π),所以任何大于2π的角度,都可以通过增加或者减少2π的倍数,将计算角度缩小在正2π范围内。于是,有了如下最简单的一组诱导公式:
$$ \sin(2k\pi + \alpha) = \sin \alpha\quad (k \in Z) $$ $$ \cos(2k\pi + \alpha) = \cos \alpha\quad (k \in Z) $$ $$ \tan(2k\pi + \alpha) = \tan \alpha\quad (k \in Z) $$ $$ \cot(2k\pi + \alpha) = \cot \alpha\quad (k \in Z) $$ $$ \sec(2k\pi + \alpha) = \sec \alpha\quad (k \in Z) $$ $$ \csc(2k\pi + \alpha) = \csc \alpha\quad (k \in Z) $$
通过以上一组诱导公式,可以将角度控制在2π以内。然后,在2π以内的变换,我们就要用到著名的诱导公式口诀:奇变偶不变,符号看象限。
对于 \( {\cfrac {k\pi}{2}} \pm \alpha (k \in Z) \) 的三角函数值:
1, 当 \(k\) 是偶数时,得到 \(\alpha\) 的同名函数值,即函数名不改变;
2, 当 \(k\) 是奇数时,得到 \(\alpha\) 相应的余函数值,即 \(\sin \to \cos ; \cos \to \sin \) ;奇变偶不变,变与不变的都是函数,然后在前面加上把 \(\alpha\) 看成锐角(大于0°而小于90°直角的角)时原函数值的符号(符号看象限,只需要记住 \(\sin\) 是1,2象限为正,\(\cos\) 是1,4象限为正即可,记忆方法就是画出函数曲线图);
3, 当k为负整数的时候,比如 \(\sin(a-\frac{\pi}{2})\) ,可以直接通过增加 \(2\pi\) 的方式,将 \(\frac{\pi}{2}\) 的倍数转变为正数;例如本例,增加 \(2\pi\) ,将表达式变为 \(\sin(a+\frac{3\pi}{2})\) 。
例如:
\(\sin (2\pi - \alpha) = \sin (\frac {4\pi}{2} - \alpha) \) ,\(k = 4\) ,偶数倍 \(\frac {\pi}{2}\) ,所以取 \(\sin\) ;当 \(\alpha\) 是锐角时,\(2\pi - \alpha \in (270^\circ,360^\circ)\) ,在第4象限,\( \sin(2\pi - \alpha) \lt 0 \) ,所以取符号为“-”;(通过变与不变之前的函数来看符号);所以 \( \sin(2\pi - \alpha) = -\sin\alpha \) 。
还有一组诱导公式,可以通过三角函数的奇偶性来理解和记忆。正弦\(\sin\)是奇函数,而余弦\(\cos\)是偶函数,于是:
$$\begin{align} \sin(-\alpha) &= -\sin\alpha \\ \cos(-\alpha) &= \cos(\alpha) \\ \tan(-\alpha) &= \frac {\sin(-\alpha)}{\cos(-\alpha)} = -\tan\alpha \\ \cot(-\alpha) &= \frac {\cos(-\alpha)}{\sin(-\alpha)} = -\cot\alpha \\ \sec(-\alpha) &= \frac {1}{\cos(-\alpha)} = \sec\alpha \\ \csc(-\alpha) &= \frac {1}{\sin(-\alpha)} = -\csc\alpha \end{align}$$
以上变换,均可看做是k=0的特殊情况。
记忆方法,就是三角函数的周期性和奇偶性,再加上一句口诀!
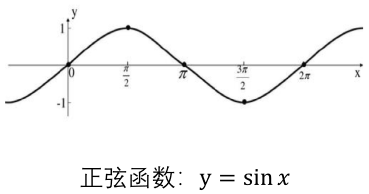
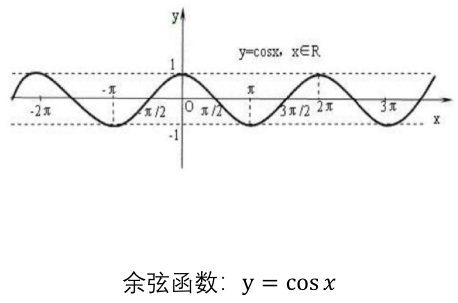
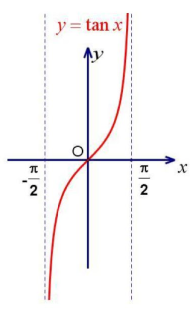
$$\sin(a+b) = \sin{a}{\cdot}\cos{b} + \cos{a}{\cdot}\sin{b}$$
基于以上公式,可以直接写出 \(\sin(a-b)\) 的展开式;
将 \(\cos(a+b)\) 写成 \(\sin(a+b+\frac{\pi}{2})\) 就可以写出其展开式;
然后再直接写出 \(\cos(a-b)\) 的展开式。
用两角和差公式推导和差化积公式:
\( \sin{a} + \sin{b} \\ = \sin(\cfrac{(a+b)}{2} + \cfrac{(a-b)}{2}) \\ \quad + \sin(\cfrac{(a+b)}{2} - \cfrac{(a-b)}{2}) \)
三角函数二倍角公式的各种推导,都可利用两角和差公式推导。
三角函数和差化积公式相对记忆难度偏大,因为里面有许多二分之一的表达式。我们可以采取一条简单的记忆路线,即先记住两角和差公式,然后用两角和差公式直接推导和差化积公式。具体如下:
1, 只需记住最重要的一个两角和差公式
对,只需记住这一个,就可以将我们常用的所有三角函数公式全部推导出来,本文主要介绍推导和差化积公式。
这个需要记住的公式为:$$\sin(a+b) = \sin{a}\cos{b}+\cos{a}\sin{b}$$
这个公式太重要了,几乎所有常用的三角函数公式都可以由它来推导。
2, 开始推导和三角函数和差化积公式
\( \sin{a} + \sin{b} \\ = \sin(\frac{(a+b)}{2} + \frac{(a-b)}{2}) \\ \quad+ \sin(\frac{(a+b)}{2} - \frac{(a-b)}{2}) \\ = \sin(\frac{a+b}{2}){\cdot}\cos(\frac{a-b}{2}) \\ \quad+ \cos(\frac{a+b}{2}){\cdot}\sin(\frac{a-b}{2}) \\ \quad + \sin(\frac{a+b}{2}){\cdot}\cos(\frac{a-b}{2}) \\ \quad- \cos(\frac{a+b}{2}){\cdot}\sin(\frac{a-b}{2}) \\ = 2{\cdot}\sin(\frac{a+b}{2}){\cdot}\cos(\frac{a-b}{2}) \)
通过两角和差公式,直接写出和差化积公式。
3, 用这一个和差化积公式,直接推导剩下的公式
\( \sin{a} - \sin{b} \\ = \sin{a} + \sin(-b) \)
\( \cos{a} + \cos{b} \\ = \sin(a + \frac{\pi}{2}) + \sin(b + \frac{\pi}{2}) \quad (..1) \)
\( \cos{a} - \cos{b} \\ = \cos{a} + \cos(b + \pi) \quad (..2) \)
公式(2)直接使用公式(1)来展开。
4, 反向使用两角和差公式推导 \(\tan{a}+\tan{b}\)
不说废话了,直接写出推导过程:
\( \tan{a}+\tan{b} \\ = \cfrac{\sin{a}}{\cos{a}} + \cfrac{\sin{b}}{\cos{b}} \\ = \cfrac{\sin{a}{\cdot}\cos{b}+\cos{a}{\cdot}\sin{b}}{\cos{a}{\cdot}\cos{b}} \\ = \cfrac{\sin(a+b)}{\cos{a}{\cdot}\cos{b}} \)
本文推导公式的过程,也是非常简单有效的记忆过程!
推导三角函数积化和差的公式,再次证明两角和差公式的重要性!具体推导就是将两角和差公式反过来应用,如下:
\( \sin{a}\cos{b} \\ = \frac{1}{2}{\cdot}[2{\cdot}\sin{a}\cos{b} \ \quad + \cos{a}\sin{b} - \cos{a}\sin{b}] \\ = \frac{1}{2}{\cdot}[\sin(a+b)+\sin(a-b)] \)
另外3个积化和差公式如下:
\( \cos{a}\sin{b} \\ = \frac{1}{2}{\cdot}[\sin(a+b)-\sin(a-b)] \)
\( \cos{a}\cos{b} \\ = \frac{1}{2}{\cdot}[\cos(a+b)+\cos(a-b)] \)
\( \sin{a}\sin{b} \\ = -\frac{1}{2}{\cdot}[\cos(a+b)-\cos(a-b)] \)
三角函数二倍角公式,可以用两角和差公式来直接推导。具体如下:
$$\begin{align} 1 - \cos{2x} &= 1 - cos(x+x) \\ &= 1 - (\cos^2{x} - \sin^2{x}) \\ &= 2{\cdot}\sin^2{x} \end{align}$$
用同样的方法,可以得到:
$$\begin{align} 1 + \cos{2x} &= 1 + cos(x+x) \\ &= 1 + (\cos^2{x} - \sin^2{x}) \\ &= 2{\cdot}\cos^2{x} \end{align}$$
\(1+\sin{2x}=(\sin{x}+\cos{x})^2 \)
\(1-\sin{2x}=(\sin{x}-\cos{x})^2 \)
最后,二倍角公式的推导过程,也是记忆过程。
三角函数半角公式的推导,主要使用二倍角公式,根据半角公式的不同的表达式,还是用到了一点点两角和差公式。如果考虑到二倍角公式也是由两角和差公式推导出来的话,所有的半角公式都可以用两角和差公式来推导,再次说明三角函数两角和差公式的重要性!
三角函数半角公式推导过程如下:
由二倍角公式可得:
$$ 1 - \cos{a} = 2{\cdot}\sin^2(\frac{a}{2}) $$
所以:
$$ \sin(\frac{a}{2}) = \pm \sqrt{\frac{1-\cos{a}}{2}} $$
同理,由二倍角公式有:
$$1 + \cos{a} = 2{\cdot}\cos^2(\frac{a}{2})$$
所以:
$$ \cos(\frac{a}{2}) = \pm \sqrt{\frac{1+\cos{a}}{2}} $$
因此:
$$ \tan(\frac{a}{2}) = \pm \sqrt{\frac{1-\cos{a}}{1+\cos{a}}} $$
另外:
$$\begin{align} \tan(\frac{a}{2}) &= \frac{\sin(\frac{a}{2})}{\cos(\frac{a}{2})} \\ &= \frac{2{\cdot}\sin(\frac{a}{2}){\cdot}\cos(\frac{a}{2})}{2{\cdot}\cos^2(\frac{a}{2})} \\ &= \frac{\sin{a}}{1+\cos{a}} \end{align}$$
上式证明,是将两角和差和二倍角公式反过来使用,上式还有另外一个表达形式:
$$\begin{align} \tan(\frac{a}{2}) &= \frac{\sin(\frac{a}{2})}{\cos(\frac{a}{2})} \\ &= \frac{2{\cdot}\sin^2(\frac{a}{2})}{2{\cdot}\sin(\frac{a}{2})\cos(\frac{a}{2})} \\ &= \frac{1-\cos{a}}{\sin{a}} \end{align}$$
以上就是所有的三角函数半角公式。
不是很清楚为什么这一组三角函数的公式叫做万能公式,不过要推导万能公式,却并不困难,推导过程用到的最重要的公式,依然是两角和差公式。具体推导过程如下:
$$\begin{align} \sin{a} &= \sin(\frac{a}{2}+\frac{a}{2}) \\ &= 2{\cdot}\sin{\frac{a}{2}}\cos{\frac{a}{2}} \\ &= \cfrac{2{\cdot}\cfrac{\sin{\frac{a}{2}}}{\cos{\frac{a}{2}}}}{\cfrac{1}{\cos^2{\frac{a}{2}}}} \\ &= \frac{2{\cdot}\tan{\frac{a}{2}}}{1+\tan^2{\frac{a}{2}}} \end{align}$$
用同样的方法,可以得到万能公式的另外1个表达式:
$$\cos{a} = \frac{1-\tan^2{\frac{a}{2}}}{1+\tan^2{\frac{a}{2}}}$$
最后,很简单的就可以得到:
$$\tan{a} = \frac{2{\cdot}\tan{\frac{a}{2}}}{1-\tan^2{\frac{a}{2}}}$$
高等数学在求部分积分的运算中,需要用到三角函数万能公式。
45度角有点特殊,这个角度的sin和cos的值可以很容易地计算出来,所以,需要记住。
计算45度角的值的方法很多,下面计算过程图:

记住下面的一组值,在很多时候,分析函数的各方面性质的时候,很有用:
\( \sin(45^o)= \cos(45^o) \\ = \sin(\frac{\pi}{4})=\cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2} \)
\( \tan(45^o)=\cot(45^o) \\ =\tan(\frac{\pi}{4})=\cot(\frac{\pi}{4})=1 \)
\( \sec(45^o)=\csc(45^o) \\ = \sec(\frac{\pi}{4})=\csc(\frac{\pi}{4})=\sqrt{2} \)
有的时候,知道这么一个值,就能够判断出函数的零点数,画出函数的曲线图。
另,在 \( [0,\frac{\pi}{4}] \)比较\(\tan{x},\sin{x}\)和\(x\)的大小,在不是趋近于0的时候,一般都有:
\(\tan{x}>x>\sin{x}\)

这个性质,有的时候在判断定积分大小时,很管用。
三角函数30度和60度的值也特殊,同时也可以轻松算出,利用一个等边三角形(正三角形)就行了。
等边三角形每个内角度数都是60度,AC垂线将角BAD分成两个30度,同时也将BD等分成BC和CD。用勾股定理就能够很容易计算出30度角和60度角的正弦和余弦值。
\(\sin{30^o}=\sin{\frac{\pi}{6}}=\cos{60^o}=\cos{\frac{\pi}{3}}=\frac{1}{2}\)
\(\sin{60^o}=\sin{\frac{\pi}{3}}=\cos{30^o}=\cos{\frac{\pi}{6}}=\frac{\sqrt{3}}{2}\)
三角函数在0,30,45,60,90这些特殊的角度时,其值都可以计算出来。
本文链接:https://cs.pynote.net/math/202204135/
-- EOF --
-- MORE --